?Existen poliedros ¡°agujereados¡± que no tengan diagonales?

En el mundo de las matem¨¢ticas podemos encontrar muchos submundos que, aunque sea parcelas muy concretas y acotadas, esconden una gran cantidad de curiosidades dignas de ser estudiadas y analizadas. Uno de esos submundos, que ser¨¢ el protagonista de este art¨ªculo, es el de los poliedros.

Como ya sabemos, podemos definir poliedro como una figura tridimensional limitada por pol¨ªgonos que encierra un volumen finito. Hay muchos poliedros que tienen caracter¨ªsticas destacables, como los regulares, los semirregulares, los arquimedianos, etc. Esta definici¨®n puede generalizarse a cualquier dimensi¨®n, y el nombre general pasar¨ªa a ser pol¨ªtopo. Como curiosidad, comentar que en dimensi¨®n cero hay un solo pol¨ªtopo regular, al igual que en dimensi¨®n uno; en dimensi¨®n dos hay infinitos pol¨ªtopos regulares (todos los pol¨ªgonos regulares); en dimensi¨®n tres tenemos cinco (los cinco poliedros regulares); en dimensi¨®n cuatro tenemos seis; y de dimensi¨®n cinco en adelante hay exactamente tres pol¨ªtopos regulares.

Volvamos a los poliedros, a los tridimensionales. De ellos ya hablamos aqu¨ª en el art¨ªculo dedicado a la f¨®rmula de Euler, y tambi¨¦n cuando analizamos qu¨¦ poliedros se pod¨ªan tetraedrizar o cuando contamos la historia de Matt Parker y el bal¨®n imposible. Hoy vamos a hablar de un poliedro muy concreto que tiene unas caracter¨ªsticas y unas propiedades bastante interesantes: el poliedro de Cs¨¢sz¨¢r.

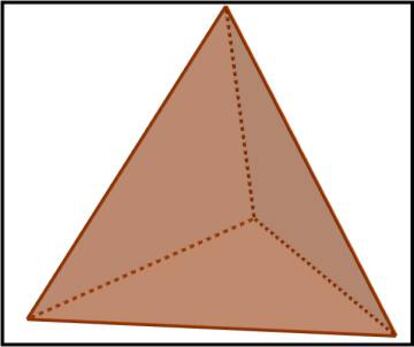
Comencemos hablando del tetraedro. Si os fij¨¢is, el tetraedro no tiene diagonales, cada pareja de v¨¦rtices est¨¢ ya unido por una arista, por lo que no hay ninguna pareja de aristas ¡°libres¡± para que sean unidas por un nuevo segmento, que es al que llamar¨ªamos ¡°diagonal¡±. Por otra parte, si imaginamos el tetraedro como una figura de plastilina, podr¨ªamos deformarlo (sin romperlo) hasta convertirlo en una esfera. Bien, pues el tetraedro es el ¨²nico poliedro deformable en una esfera que cumple que no tiene diagonales.

En 1949, el matem¨¢tico h¨²ngaro ?kos Cs¨¢sz¨¢r se pregunt¨® sobre si habr¨ªa alg¨²n poliedro no deformable en una esfera (esto es, que tuviera alg¨²n ¡°agujero¡± que impidiera convertirlo en una esfera) que cumpliera lo mismo que el tetraedro, que no tuviera diagonales. Y lo encontr¨®. En su trabajo A polyhedron without diagonals, ?kos responde a esta pregunta demostrando que s¨ª existe tal poliedro, que acab¨® llam¨¢ndose poliedro de Cs¨¢sz¨¢r:

Como en la imagen no se aprecia bien el poliedro en toda su extensi¨®n, os dejo el siguiente v¨ªdeo (tomado de la Wikipedia) en el que podemos verlo mucho mejor y, adem¨¢s, ver tambi¨¦n su desarrollo plano:

Este curioso poliedro es no convexo (tiene un agujero), y posee 7 v¨¦rtices, 21 aristas y 14 caras, todas ellas tri¨¢ngulos. No cumple la f¨®rmula de Euler, ya que

14 ¨C 21 ¨C 7 = 0 ¡Ù 2

y, como puede verse en el v¨ªdeo, no tiene diagonales: todas las parejas posibles de v¨¦rtices est¨¢n ya unidos con una arista.

Como curiosidad, y hasta donde yo s¨¦, no se conocen poliedros (convexos o no) que no tengan diagonales salvo el tetraedro y este poliedro de Cs¨¢sz¨¢r. Si alguien tiene informaci¨®n nueva a este respecto, estaremos muy agradecidos si la comparte con nosotros en los comentarios.

Creo que es bastante evidente que el poliedro de Cs¨¢sz¨¢r tiene una forma algo extra?a, por lo que se podr¨ªa pensar que es complicado de construir. ??Nada de eso!! De hecho no es demasiado dif¨ªcil de montar¡­si nos dan una buena plantilla de su desarrollo plano en dos dimensiones que nos ayude a ello. Y en El Aleph estamos para eso.

Podr¨ªais reconstruir la que se ve en el v¨ªdeo, pero seguro que prefer¨ªs que os la den ya hecha. Pues aqu¨ª os dejo una muy buena plantilla del poliedro de Cs¨¢sz¨¢r junto con alguna peque?a instrucci¨®n para montarlo, gracias a la magn¨ªfica web CutOutFoldUp: plantilla del poliedro de Cs¨¢sz¨¢r en CutOutFoldUp. Desde este blog, os animamos a que os descargu¨¦is la plantilla e intent¨¦is montar el poliedro, y a que, si quer¨¦is, nos dej¨¦is una foto de vuestra obra maestra en los comentarios.

Relacionado con este poliedro tenemos otro tambi¨¦n con una forma y unas caracter¨ªsticas muy curiosas: el poliedro de Szilassi, descubierto por el matem¨¢tico Lajos Szilassi en 1977. Este poliedro es el dual del poliedro de Cs¨¢sz¨¢r. Os dejo que investigu¨¦is sobre c¨®mo construirlo y sobre sus propiedades.

Y, para terminar, una curiosidad relacionada con la tetraedrizaci¨®n de la que hablamos en este art¨ªculo. ?Es tetraedrizable el poliedro de Cs¨¢sz¨¢r? Pues la respuesta es s¨ª, el poliedro de Cs¨¢sz¨¢r se puede tetraedrizar. Pod¨¦is verlo en Wolfram Demonstrations Project.