Juego parece...

Despu¨¦s de habernos divertido con el Juego del Drago y de hacerle un tributo al cubo de Rubik, el rompecabezas m¨¢s famoso de la historia, continuamos hablando de juegos¡­o no. Sigue leyendo y entender¨¢s qu¨¦ quiero decir.

Estoy seguro de que en alguna ocasi¨®n te han propuesto jugar a alg¨²n juego sencillo y, despu¨¦s de unas cuantas partidas, e independientemente de la estrategia que hayas seguido, no has conseguido ganar ni una sola vez. Es posible entonces que ese juego tenga una estrategia ganadora para uno de los jugadores (ya sea el primero o el segundo) y la persona que te lo propuso conozca dicha estrategia y se haya colocado en la posici¨®n del jugador que acabar¨¢ ganando si ¡°juega bien¡±.

Pongamos un ejemplo. Imagina que tenemos 15 palillos y jugamos alternativamente a retirar uno o dos palillos en cada turno, ganando el jugador que se lleve el ¨²ltimo palillo. Como soy un caballero, te dejo comenzar a ti. ?Qu¨¦ har¨ªas? Puedes hacer alguna prueba t¨² mismo antes de seguir leyendo.

?Ya? Despu¨¦s de algunas pruebas, y pensando un poquito, te habr¨¢s dado cuenta de que si yo, segundo jugador, juego convenientemente t¨², primer jugador, nunca ganar¨¢s una partida de este juego. La raz¨®n es que hay una estrategia que asegura que el segundo jugador ganar¨¢ siempre. Esta estrategia es muy simple: si t¨² coges un palillo, yo despu¨¦s cojo dos; y si t¨² coges dos palillos, yo despu¨¦s cojo uno. As¨ª siempre se habr¨¢n retirado tres palillos cada vez que haya jugado un turno cada uno, y como 15 es m¨²ltiplo de 3 yo, segundo jugador, soy el ¨²nico que puedo llevarme el ¨²ltimo palillo.

M¨¢s informaci¨®n

Si Dios tuviera un n¨²mero, ?cu¨¢l ser¨ªa?

El Juego del Drago

Hay much¨ªsimos juegos sencillos para los cuales se conoce estrategia ganadora (o no perdedora, si el juego permite un empate), y muchos para los que se sabe que dicha estrategia existe aunque no se conozca. As¨ª que ten cuidado y, si ves que nunca ganas, analiza el juego y prueba a pedir cambiar de posici¨®n, ya que esa ser¨¢ una de las claves.

Ahora, en uno de estos juegos podr¨ªas no perder siempre, ya que quiz¨¢s el jugador que te lo propone no conoce la estrategia ganadora (o no perdedora). Por ejemplo, para el tres en raya existe una estrategia no perdedora tanto para el primer jugador como para el segundo, por lo que todas las partidas deber¨ªan acabar en empate si ambos jugadores ¡°juegan bien¡±. Pero la realidad es que a veces gana uno de los jugadores porque el otro no conoce dicha estrategia o porque comete alg¨²n error. Por tanto, en estos juegos todav¨ªa te queda alguna esperanza de ganar.

Pero estos no son los juegos de los que yo quer¨ªa hablar hoy. Quer¨ªa presentaros unos juegos que parecen juegos pero que en realidad no son juegos. Voy a poner un ejemplo para intentar aclarar este l¨ªo.

Volvamos a los palillos, elementos muy socorridos para este tipo de divertimentos. Ahora tenemos 20 de ellos, y en cada turno un jugador puede retirar un palillo, tres palillos o cinco palillos a su elecci¨®n. Gana quien se lleve el ¨²ltimo palillo. ?Te interesa ser el primer jugador o el segundo? Elegida ya la posici¨®n, ?qu¨¦ estrategia utilizar¨ªas para ganar? De nuevo, te animo a que hagas alguna prueba por tu cuenta antes de seguir leyendo.

?Qu¨¦ tal las pruebas? Seguro que ya has descubierto el ¡°truco¡±, pero por si acaso te lo cuento yo: te interesa ser el segundo jugador, y ganar¨¢s siempre sin importar la estrategia que utilices. Si nos fijamos, cada jugador puede retirar solamente una cantidad impar de palillos, por lo que el ¨²nico que puede dejar un n¨²mero par de palillos en la mesa es el segundo jugador. El jugador que gana, el que se lleva el ¨²ltimo palillo, deja cero palillos en la mesa. Y como cero es par, est¨¢ claro que el ¨²nico que puede ganar es el que puede dejar un n¨²mero par de palillos, el segundo jugador en este caso.

Y no importa la estrategia que use, da lo mismo la cantidad de palillos que tome en cada turno, acabar¨¢ ganando siempre. ?Veis la diferencia con los juegos anteriores? All¨ª hab¨ªa que seguir una estrategia para ganar, pero aqu¨ª el segundo jugador gana s¨ª o s¨ª sin necesidad de tirar de estrategia, y el primer jugador no puede hacer nada por evitarlo. Es algo as¨ª como que el ganador est¨¢ ya determinado por las propias reglas del juego, independientemente de los movimientos que hagan cada uno de los jugadores.

Por eso dec¨ªa antes que estos ¡°juegos¡± en realidad no son juegos en un sentido estricto, ya que no dan la opci¨®n de ¡°jugar¡±. Por ello, en ocasiones suelen llamarse pseudojuegos. Veamos otro ejemplo, ahora con monedas.

Supongamos que tenemos nueve monedas de 50 c¨¦ntimos y seis monedas de 10 c¨¦ntimos:

El juego, para dos jugadores, consiste en retirar monedas alternativamente con las siguientes reglas:

- En cada turno se puede retirar dos monedas iguales o dos monedas distintas.

- Si se retiran dos monedas iguales, el jugador a?ade una moneda de 50 c¨¦ntimos a las que queden.

- Si se retiran dos monedas distintas, el jugador deja en su lugar una moneda de 10 c¨¦ntimos.

Como pod¨¦is ver, en cada turno el n¨²mero de monedas disminuye en una unidad, por lo que llegar¨¢ el momento en el que s¨®lo quedar¨¢ una moneda. Si esa moneda es de 10 c¨¦ntimos gana el primer jugador; si es de 50 c¨¦ntimos, gana el segundo jugador. ?Qu¨¦ jugador elegir¨ªas ahora? ?Y qu¨¦ estrategia seguir¨ªas? Como antes, te animo a que pruebes por ti mismo antes de seguir¡­

¡­?C¨®mo han ido las pruebas? ?Sabes ya a qui¨¦n elegir y qu¨¦ hacer? Seguro que s¨ª, pero ve¨¢moslo. Vamos a fijarnos en el n¨²mero de monedas de 10 c¨¦ntimos que tendremos en cada momento. Comenzamos con seis, n¨²mero par, y despu¨¦s pueden pasar dos cosas:

- Que quitemos dos (lo de las dos iguales), con lo que no a?adimos ninguna m¨¢s de 10 c¨¦ntimos.

- Que quitemos una (si quitamos dos distintas), y por tanto tengamos que a?adir otra.

Esto significa que en todo momento hay un n¨²mero par de monedas de 10 c¨¦ntimos, lo que nos lleva a que, juguemos como juguemos, las monedas de 10 c¨¦ntimos acabar¨¢n desapareciendo (el ¡°caso l¨ªmite¡± es que queden solamente dos monedas de 10 c¨¦ntimos, que se quitar¨ªan y se sustituir¨ªan por una de 50 c¨¦ntimos). La consecuencia de esto es que la ¨²ltima moneda ser¨¢, irremediablemente, de 50 c¨¦ntimos, independientemente de c¨®mo juegue cada uno de los jugadores en cada uno de sus turnos. Por tanto, de nuevo estamos ante un pseudojuego que, con estas reglas, siempre ganar¨¢ el segundo jugador.

Y terminamos con otro juego, m¨¢s concretamente con una variante del Juego del Drago del que habl¨¢bamos hace un par de semanas. Se trata de la variante conocida como Brussels Sprouts (Brotes de Bruselas, o tambi¨¦n Coles de Bruselas), y en vez de comenzar con unos cuantos puntos comienza con un cierto n¨²mero de cruces (una o m¨¢s). Las reglas son las siguientes:

- En cada turno, el jugador traza una l¨ªnea (recta, curva¡­) que une dos salientes de alguna de las cruces (de la misma o de dos distintas) y a?ade una peque?a rayita (es decir, dos salientes m¨¢s) en alg¨²n punto de la l¨ªnea que traz¨® inicialmente.

- Una l¨ªnea no puede cortar a otra l¨ªnea ya dibujada ni a ninguna otra cruz que no sea la inicial o la final.

- Gana el jugador que trace la ¨²ltima l¨ªnea que pueda trazarse.

Os dejo un ejemplo de dos primeros movimientos en una partida de Brussels Sprouts que comienza con dos cruces:

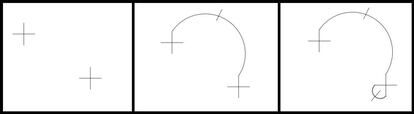
La cuesti¨®n es ver si esto es un juego o un pseudojuego y, en ese caso, qui¨¦n gana y de qu¨¦ depende que gane. Se puede encontrar informaci¨®n de este juego en internet, pero lo ideal es que prob¨¦is por vuestra cuenta y que, al menos, conjetur¨¦is la soluci¨®n sin buscarla antes. Pod¨¦is contarnos vuestros progresos en los comentarios.

Espero que os haya gustado conocer este tipo de juegos que no son juegos, y si ya sab¨ªais de ellos y conoc¨¦is alguno m¨¢s os agradecer¨ªamos mucho que nos hablarais de ellos en los comentarios.