Las cartas boca abajo
No tiene que ver con la famosa obra teatral de Buero Vallejo, sino con un elegante acertijo popularizado por el cine
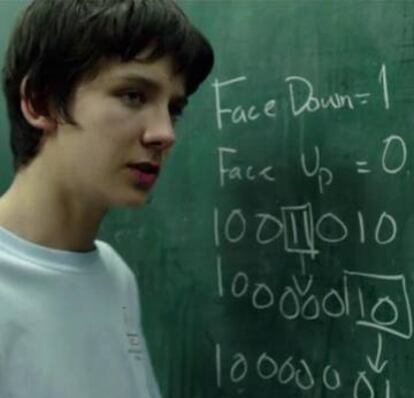
En el cubo Soma, del que nos ocup¨¢bamos la semana pasada, hay una de las siete piezas, que solo puede ir en una posici¨®n, y eso es lo que tienen en com¨²n las 240 soluciones distintas del rompecabezas. ?Cu¨¢l es esa pieza y por qu¨¦ ha de ir siempre en la misma posici¨®n?
Adem¨¢s de reconstruir el cubo, con las piezas del Soma se pueden formar una gran cantidad de estructuras interesantes. En el primer comentario de la semana pasada, Carlos Gaceo propone un acertijo tomado de la revista Investigaci¨®n y Ciencia: determinar, de entre una docena de construcciones que incluyen las siete piezas, cu¨¢l es imposible (ver figura del comentario 1 del art¨ªculo anterior). Sirva como pista que no es necesario disponer f¨ªsicamente de las piezas para hallar la soluci¨®n.
Cine y matem¨¢ticas
Las matem¨¢ticas no tienen mucha presencia en el cine, y cuando llegan a la gran pantalla, a menudo se ofrece de ellas una visi¨®n un tanto m¨ªstica o esot¨¦rica que poco tiene que ver con la realidad. No es el caso de x + y (A Brilliant Youg Mind), pel¨ªcula brit¨¢nica que cuenta con realismo y sensibilidad la historia de un ni?o autista superdotado que se prepara para participar en una olimp¨ªada matem¨¢tica. Uno de los problemas que el protagonista resuelve de forma brillante es el siguiente:
Colocamos veinte cartas en una ¨²nica fila, todas boca abajo. Un movimiento consiste en dar la vuelta a una carta que est¨¢ boca abajo (que en el primer movimiento es cualquiera de las veinte) y acto seguido a la que est¨¢ a su derecha. Demostrar que, independientemente de las cartas elegidas, esta secuencia de movimientos es finita.
Y otro problema tomado de la misma pel¨ªcula:
?Existen infinitos pares de n¨²meros naturales (m, n) tales que m divide a n al cuadrado m¨¢s uno, y n divide a m al cuadrado m¨¢s uno?
Y para terminar, un metaacertijo para nuestras/os seguidoras/es habituales: ?qu¨¦ tiene que ver todo esto con lo visto en los art¨ªculos de las ¨²ltimas semanas? En este caso, el criterio de continuidad que suele llevar de un art¨ªculo al siguiente no es tan evidente como de costumbre; pero seguro que nuestras/os sagaces lectoras/es lo descubren.
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
Sobre la firma
