La matem¨¢tica ucraniana que podr¨ªa haber ganado la medalla Fields

Esta nueva edici¨®n del Congreso Internacional de Matem¨¢ticos, que termin¨® el pasado 9 de agosto en R¨ªo de Janeiro, ha tra¨ªdo consigo varias sorpresas: es la primera vez que se roba la Medalla Fields de uno de los premiados, como le pas¨® a Caucher Birkar, y se le concede una segunda durante el evento. Adem¨¢s, los galardonados con la medalla han sido bastante inesperados: si bien la obtuvieron algunos de los favoritos, como Peter Scholze, tambi¨¦n aparecieron algunos que no estaban en las apuestas, como el propio Birkar y no lo hicieron algunos que s¨ª eran sobradamente populares. Entre ellos brillaba el nombre de una mujer: Maryna Viazovska, que de haber ganado se habr¨ªa convertido en la segunda mujer en hacerlo, despu¨¦s de que Maryam Mirzakhani obtuviera el galard¨®n en 2014.

A Maryna Viazovska (Kiev, Ucrania; 1984) no le faltaban razones para estar entre las favoritas: defendi¨® su tesis doctoral en 2013 en la Universidad de Bonn (Alemania) y ya es catedr¨¢tica en la prestigiosa universidad Polit¨¦cnica Federal de Lausanne (Suiza); en 2016 resolvi¨® un famoso problema geom¨¦trico sobre empaquetamiento de esferas, para dimensi¨®n ocho, y lo public¨® en Annals of Mathematics, una de las revistas m¨¢s prestigiosas de matem¨¢ticas. Una semana despu¨¦s lo hizo para dimensi¨®n 24, en un trabajo conjunto con otros colaboradores, que tambi¨¦n public¨® la misma revista. El problema de empaquetamiento de esferas aparece en cristalograf¨ªa, pero tambi¨¦n en teor¨ªa de la informaci¨®n desarrollada por Claude Shannon y en el Big Data. Podemos imaginar su formulaci¨®n m¨¢s sencilla al colocar las naranjas en una fruter¨ªa: ?cu¨¢l es la mejor manera de hacerlo, de forma que ocupen el menor espacio posible? Habitualmente est¨¢n dispuestas en forma piramidal, siguiendo una estructura arm¨®nica y sim¨¦trica, y de hecho esta es la manera ¨®ptima de ordenarlas. Esta es una de las disposiciones con mayor densidad, es decir, que deja menos huecos entre las naranjas. Demostrar matem¨¢ticamente que esto es cierto no es tan sencillo como puede parecer.

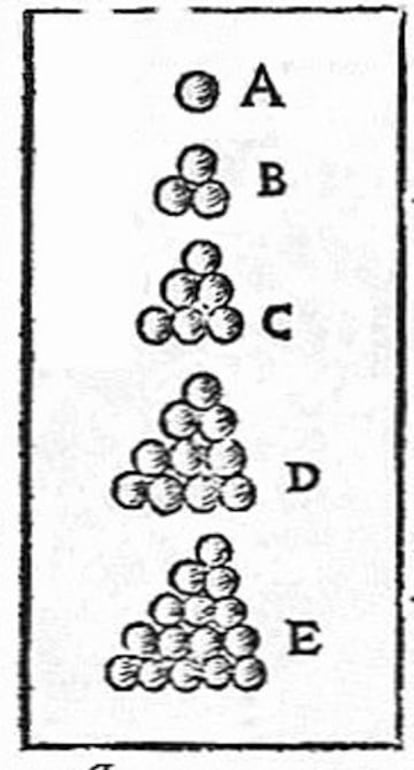
En una dimensi¨®n (o sea, en una recta) el an¨¢logo de una esfera es un intervalo (se puede imaginar como un palillo). En este caso se pueden colocar dos palillos seguidos sin dejar ning¨²n espacio entre ellos, de manera que ocupan el 100% del espacio y suponen la soluci¨®n ¨®ptima. En dos dimensiones el problema se traduce en agrupar monedas sobre una mesa de forma ¨®ptima, y la disposici¨®n hexagonal, en forma de panal, es la que consigue mayor densidad (con una densidad del 91% aproximadamente). El matem¨¢tico noruego Axel Thue anunci¨® en 1892 esta soluci¨®n (y que es mejor que cualquier otra), pero no fue demostrada hasta 1941 por el matem¨¢tico h¨²ngaro L¨¢szl¨® Fejes T¨®th.?

En dimensi¨®n tres (el problema de las naranjas) hay dos soluciones posibles (con densidad de un 74%), que fueron conjeturadas por Kepler. La demostraci¨®n de su conjetura form¨® parte de la famosa lista de problemas de Hilbert y hasta 1998 no fue demostrada por Thomas Hales, con una prueba asistida por ordenador que fue corroborada tras un largo proceso en 2005.

De forma general el problema no est¨¢ resuelto. Viazovska ha resuelto los casos de dimensi¨®n ocho, donde la densidad m¨¢xima de empaquetamiento es aproximadamente del 25% (o sea aproximadamente el 75% son ¡°huecos"), y dimensi¨®n 24 donde la densidad m¨¢xima es del 0.1%. Para hacerlo, Viazovska ha recurrido a la teor¨ªa de simetr¨ªas (teor¨ªa de Lie) e incluso a una funci¨®n m¨¢gica, como ella misma la describe. Ilustraci¨®n 6: Viazovska durante su charla invitada en el ICM (Fuente: ICM) Por estas contribuciones Viazovska ha recibido numerosos reconocimientos, como el premio Salem, el Clay, el europeo en combinatoria, el SASTRA Ramanujan y el New Horizons Prize in Mathematics (creado, entre otros, por el fundador de FacebookMark Zuckerberg y rechazado por Peter Scholze un par de a?os antes). Esta colecci¨®n de galardones podr¨ªa haber sido coronada con la reina de todos los premios en matem¨¢ticas, la medalla Fields. Esperemos que en la ciudad de San Petersburgo, donde se celebrar¨¢ el pr¨®ximo Congreso Internacional de Matem¨¢ticos en 2022, lo consiga. Esta ser¨¢ su ¨²ltima oportunidad para hacerlo, ya que a¨²n no habr¨¢ cumplido los 40 a?os, el l¨ªmite de edad del premio.

Eva Miranda es profesora ICREA Academia en la Universidad Polit¨¦cnica de Catalunya, miembro de la BGSMath, doctora vinculada en el CSIC-ICMAT y Chercheur Affili¨¦ en el Observatorio de Par¨ªs.

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".