Del tri¨¢ngulo sagrado al teorema de Pit¨¢goras

Mucho antes de que Pit¨¢goras (o alguno de sus disc¨ªpulos) demostrara su famoso teorema, los babilonios, los indios y los egipcios conoc¨ªan -y utilizaban eficazmente- las propiedades del tri¨¢ngulo de lados 3, 4 y 5, que se consideraba sagrado. Lo m¨¢s notable de este tri¨¢ngulo es que el ¨¢ngulo opuesto al lado mayor es recto, y no hace falta se?alar la importancia del ¨¢ngulo recto en todo tipo de mediciones y construcciones. En el antiguo Egipto, el tri¨¢ngulo de proporciones 3-4-5 m¨¢s utilizado en arquitectura y agrimensura era el de lados iguales a 15, 20 y 25 codos respectivamente (unos 7.5, 10 y 12.5 metros), llamado ¡°tri¨¢ngulo is¨ªaco¡± en honor a la diosa Isis, que ya se utiliz¨® en la construcci¨®n de la pir¨¢mide de Kefr¨¦n, en el siglo XXVI a. C. Pero fueron los pitag¨®ricos quienes, dos mil a?os despu¨¦s, demostraron el teorema y le dieron su conocida expresi¨®n can¨®nica:

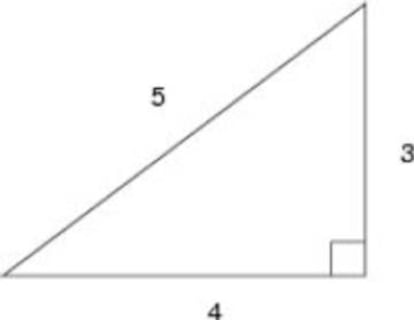
¡°En todo tri¨¢ngulo rect¨¢ngulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa¡±.

El ¨¢ngulo recto es un elemento fundamental de nuestro entorno f¨ªsico, hasta el punto de que el gran arquitecto Le Corbusier lo denomin¨® ¡°nuestro pacto de solidaridad con la naturaleza¡± y le dedic¨® un extenso -e intenso- poema; he aqu¨ª un fragmento:

Erguido sobre el plano terrestre / de las cosas comprensibles, / contraes con la naturaleza un pacto / de solidaridad: es el ¨¢ngulo recto. / De pie vertical ante la mar, / hete ah¨ª sobre tus piernas

Desde el momento en que se irguieron sobre sus patas traseras, los primeros hom¨ªnidos debieron cobrar plena conciencia del binomio horizontal-vertical, o lo que es lo mismo, de la perpendicularidad.

Es probable que las primeras demostraciones del teorema de Pit¨¢goras fueran geom¨¦tricas, ya que los pitag¨®ricos lo ve¨ªan como una relaci¨®n de los cuadrados construidos sobre los tres lados del tri¨¢ngulo rect¨¢ngulo m¨¢s que como una ecuaci¨®n algebraica. Una de las demostraciones m¨¢s elegantes es la que ilustra la figura (que tambi¨¦n se encuentra representada en algunos documentos chinos muy antiguos).

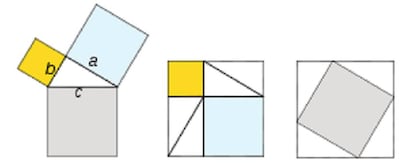
El cuadrado del centro y el de la derecha son iguales. El de la derecha est¨¢ formado por el cuadrado de lado igual a la hipotenusa y cuatro tri¨¢ngulos iguales al original; el del centro, por dos cuadrados de lados iguales, respectivamente, a ambos catetos y cuatro tri¨¢ngulos iguales al original; por lo tanto, el ¨¢rea del cuadrado mayor es igual a la suma de las ¨¢reas de los dos menores, o lo que es lo mismo, a² + b² = c².

La demostraci¨®n que encontramos con frecuencia en los libros de geometr¨ªa actuales (atribuida al propio Pit¨¢goras) se basa en la semejanza de tri¨¢ngulos.

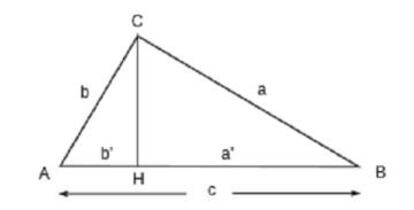
Los tri¨¢ngulos ABC y ACH son semejantes porque ambos son rect¨¢ngulos y tienen en com¨²n el ¨¢ngulo A, y por tanto sus lados son proporcionales, luego b¡¯/b = b/c, de donde b² = cb¡¯. Tambi¨¦n son semejantes ABC y BCH, pues tienen en com¨²n el ¨¢ngulo B, luego a¡¯/a = a/c, de donde a² = ca¡¯. Sumando ambas igualdades: a² + b² = ca¡¯ + cb¡¯ = c(a¡¯ + b¡¯) = c².

De Pit¨¢goras a Fermat

La f¨®rmula pitag¨®rica a² + b² = c² invita a preguntarse qu¨¦ pasa si la generalizamos a otros exponentes y la convertimos en aⁿ + bⁿ = cⁿ, donde n es un n¨²mero entero cualquiera. Pues bien, en 1637 Pierre de Fermat lleg¨® a la conclusi¨®n de que para n mayor que 2 no existen tres n¨²meros naturales (enteros y positivos) a, b, c tales que se cumpla esa igualdad. Fermat escribi¨® en el margen de un libro que hab¨ªa encontrado una demostraci¨®n ¡°admirable¡± de dicho teorema; pero nunca se encontr¨® tal demostraci¨®n, y los expertos dan por supuesto que Fermat se equivoc¨®¡­ o quiso gastarle una broma a la comunidad matem¨¢tica. De hecho, el teorema permaneci¨® en estado de conjetura durante tres siglos y medio, hasta que, tras numerosos intentos, fue demostrado por Andrew Wiles en 1995.

¡°He encontrado una demostraci¨®n realmente admirable, pero no cabe en el exiguo margen de este libro¡±, escribi¨® Fermat. Tambi¨¦n en esto el tiempo le dio la raz¨®n: la demostraci¨®n de Wiles ser¨ªa dif¨ªcil de encajar en los m¨¢rgenes de un libro, pues ocupa unas 100 p¨¢ginas.

F¨®rmulas Magistrales es un secci¨®n de Carlo Frabetti dedicada a explicar las principales f¨®rmulas de las matem¨¢ticas y la f¨ªsica, su origen, evoluci¨®n y significado preciso.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra Newsletter