Trenzas matem¨¢ticas para guardar secretos

Aunque la criptograf¨ªa es el arte de comunicar de manera secreta, tambi¨¦n podr¨ªamos decir que es la ciencia de los desaf¨ªos. As¨ª, la idea principal para transmitir informaci¨®n de forma segura por internet es que podemos probar que somos quienes decimos ser, resolviendo un reto. Por ejemplo, para acceder al correo o redes sociales usamos contrase?as. Si alguien quiere entrar a nuestra cuenta, su desaf¨ªo consiste en averiguar la clave. Si esta es suficientemente complicada, averiguarla deber¨ªa ser tan dif¨ªcil como encontrar una aguja en un pajar.

Habitualmente la seguridad inform¨¢tica se basa en desaf¨ªos matem¨¢ticos que son f¨¢ciles de resolver si uno sabe c¨®mo se han creado, pero muy complejos de solucionar sin esa informaci¨®n adicional. Ahora bien, si los ordenadores cu¨¢nticos se desarrollan lo suficiente podr¨¢n resolver algunos de estos retos sin necesidad de la informaci¨®n extra, por lo que urge encontrar nuevos est¨¢ndares criptogr¨¢ficos resistentes a la computaci¨®n cu¨¢ntica. El NIST (National Institute of Standards and Technology) inici¨® hace dos a?os un concurso para dar con ellos. Una de las propuestas, WalnutDSA, es un algoritmo de firma digital basado en una estructura algebraica llamada grupo.

En matem¨¢ticas, un grupo es un conjunto con una operaci¨®n asociativa. Los n¨²meros enteros {¡­,-3,-2,-1,0,1,2,..} con la operaci¨®n de sumar, son un grupo. Las fracciones (sin el cero) con la multiplicaci¨®n forman otro grupo. La estructura de grupo puede aparecer de formas muy curiosas e inesperadas. Por ejemplo, para cada n¨²mero natural n, hay un grupo llamado grupo de trenzas?en n cuerdas cuyos elementos son dibujos como el de abajo (aqu¨ª hemos tomado n = 4)

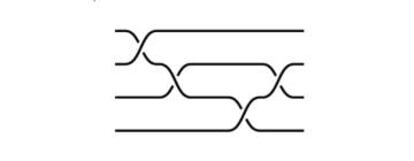
Cada dibujo representa un elemento del grupo de trenzas (podemos pensar que cada dibujo es un n¨²mero). Pero hay que tener en cuenta que en una trenza se pueden deslizar los cruces en las cuerdas, y sigue siendo la misma trenza, por lo que dibujos diferentes representan el mismo elemento. Por ejemplo, los siguientes pares de dibujos representan al mismo grupo de cuatro cuerdas.

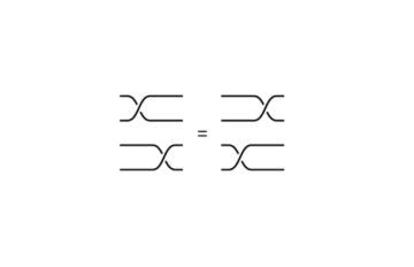
La operaci¨®n entre las trenzas es de lo m¨¢s sencillo. Unimos el final de las cuerdas de un dibujo con el principio de las cuerdas de otro dibujo para obtener una nueva trenza. Usamos + para denotar la operaci¨®n. Aqu¨ª un ejemplo.

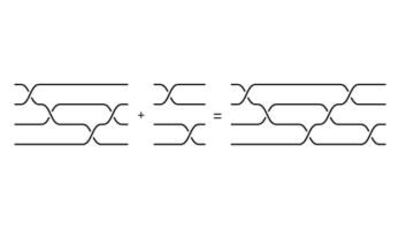
Para que sea un grupo ha de cumplir ciertas propiedades. Primero, debe haber un elemento especial, que es neutro, que al operarlo con cualquier elemento, lo deja como estaba. El cero es el neutro para la suma de n¨²meros, y el 1 lo es para la multiplicaci¨®n de fracciones. En el caso de las trenzas de n cuerdas, el elemento neutro es el dibujo de n cuerdas sin trenzar. La segunda propiedad es la existencia de inversos. Al operar un elemento con su inverso, se obtiene el neutro. El inverso de 3 respecto la suma es -3, y de 4, respecto a la multiplicaci¨®n, es ?. En nuestro caso, el inverso consiste en ¡°desenredar¡± las cuerdas. Por ejemplo, con tres cuerdas, si tenemos la trenza en la que la cuerda 2 pasa sobre la cuerda 3, su inverso ser¨¢ la trenza que pasa la cuerda 3 sobre la cuerda 2. Su unimos estos dos dibujos y estiramos de los extremos, obtenemos tres cuerdas sin trenzar.?

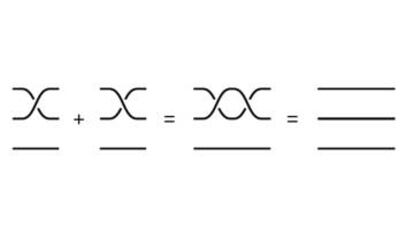
Ahora que ya sabemos que es un grupo, podemos usarlo para plantear ecuaciones y usarlas como desaf¨ªos criptogr¨¢ficos. Las primeras propuestas para aplicar las trenzas a la criptograf¨ªa datan de 1999 y 2000 y el desaf¨ªo para conseguir seguridad se basaba en resolver la llamada ecuaci¨®n de conjugaci¨®n, que tiene forma a + x = x + b d¨®nde a y b son trenzas conocidas y x es una trenza inc¨®gnita. Sin embargo, durante los a?os 2000 varios equipos de matem¨¢ticos encontraron algoritmos (1, 2, 3) para resolver esta ecuaci¨®n y finalmente esas propuestas fueron desechadas.

Ahora el algoritmo WalnutDSA las recupera para la firma digital. Para que alguien falsifique una firma deber¨ªa ser capaz de resolver ecuaciones que combinan matrices y trenzas, lo que es un reto muy complicado, no solo para los ordenadores actuales sino tambi¨¦n, seg¨²n afirman los autores del protocolo, para ordenadores cu¨¢nticos.

Adem¨¢s del grupo de trenzas, existen otros grupos interesantes en los que plantear criptosistemas. Un ejemplo popular es el de los grupos polic¨ªclicos o los graph groups en los que es f¨¢cil codificar problemas de grafos. La idea es siempre la misma: si encuentras un desaf¨ªo que los matem¨¢ticos no son capaces de resolver de forma eficiente, puede ser que hayas topado con un diamante para la criptograf¨ªa.

Yago Antol¨ªn es Ayudante Doctor en la Universidad Aut¨®noma de Madrid y miembro del ICMAT.

Delaram Kahrobaei es Directora de Ciberseguridad en el departamento de ciencias de la computaci¨®n de la Universidad de York (Reino Unido).

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n:?gata Tim¨®n (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter