?Qui¨¦n va a ganar las elecciones generales?

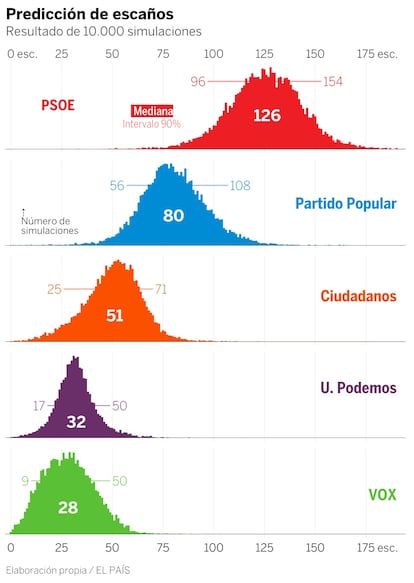
Seg¨²n nuestro modelo de predicci¨®n, el PSOE rondar¨ªa los 126 diputados en las elecciones del d¨ªa 28 de abril, seguido del PP (80), Ciudadanos (51), Unidas Podemos (32) y Vox (28).

Estos pron¨®sticos se calculan con 15.000 simulaciones de un modelo estad¨ªstico. El modelo se alimenta del promedio de encuestas y tiene en cuenta su precisi¨®n hist¨®rica. Al final se puede consultar la metodolog¨ªa.

Qui¨¦n alcanzar¨¢ la mayor¨ªa. Para escoger presidente y gobernar son necesarios 176 esca?os. ?Qu¨¦ partidos tienen probabilidades de sumar los suficientes? Las encuestas no pueden responder esa pregunta, pero este modelo s¨ª.

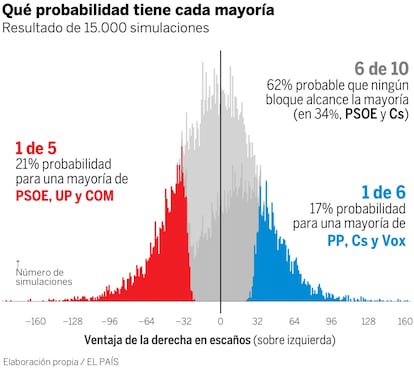
La derecha tiene un 17% de probabilidades de alcanzar la mayor¨ªa (1 opci¨®n de 6) y la izquierda un 21% (1 de 5). En el 62% restante de las veces (5 de 8) ning¨²n bloque suma 176 diputados. Son unas elecciones muy inciertas.

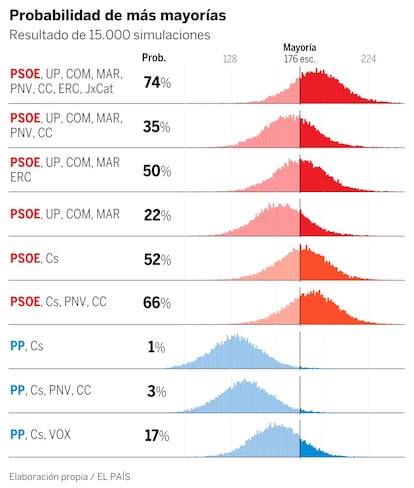
La tabla siguiente muestra otras combinaciones:

Las 15.000 simulaciones partido a partido. El gr¨¢fico muestra la distribuci¨®n de esca?os en cada simulaci¨®n. Ah¨ª puede verse la incertidumbre de las encuestas. El PSOE ronda los 127 esca?os, pero su intervalo (al 90%) va de 96 a 154 diputados. Hay un 5% de probabilidades de que se salga por abajo y otro 5% de que lo haga por arriba. Estas horquillas pueden parecer excesivas, pero no son caprichosas: reflejan el grado de precisi¨®n de las encuestas en el pasado.

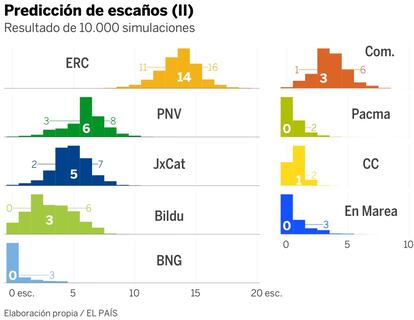
Aqu¨ª se muestra el resultado del resto de partidos:

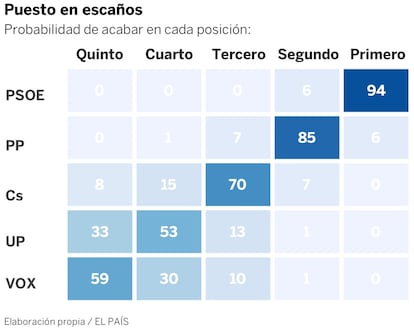
La lucha por cada puesto. En la tabla se representa la probabilidad que tiene cada partido de quedar en cada puesto. El PSOE tiene casi asegurado ser primero, pero la competici¨®n por abajo est¨¢ muy abierta. Vox es quinto en 6 de cada 10 simulaciones, cuarto en 3 de cada 10 y tercero un 10% de las veces.

Los esca?os en juego por provincias

?Quiere saber qu¨¦ diputados est¨¢n en juego en su provincia? Consulte este especial que hemos preparado a partir de los datos de nuestro modelo electoral.

Una newsletter de encuestas

?Quieres seguir las elecciones con todos los datos? Suscr¨ªbete a la newsletter de Kiko Llaneras y rec¨ªbela en tu correo.

Metodolog¨ªa. Las predicciones las produce un modelo estad¨ªstico basado en sondeos y en su precisi¨®n hist¨®rica. El modelo es similar al que usamos en M¨¦xico, Francia, el Reino Unido, Andaluc¨ªa o Catalu?a. Funciona en cuatro pasos: 1) agregar y promediar las encuestas, 2) proyectar ese promedio sobre cada provincia, 3) incorporar la incertidumbre esperada, y 4) simular 15.000 elecciones para repartir esca?os y calcular probabilidades.

Paso 1. Promedio de encuestas. Nuestro promedio tiene en cuenta decenas de sondeos para mejorar su precisi¨®n. El promedio est¨¢ ponderado para dar distinto peso a cada encuesta seg¨²n tres factores: el tama?o de la muestra, la casa encuestadora y la fecha. Los detalles pueden consultarse en esta p¨¢gina web.

Paso 2. Proyectar el voto a cada provincia. Antes de calcular los esca?os es necesario estimar el porcentaje de votos de cada partido en cada provincia. Para hacerlo, se usan los resultados de las elecciones de 2016 y algunos ajustes con encuestas provinciales.

El voto nacional de PP, PSOE, Cs, UP, ERC, JxCat, PNV, Bildu, Pacma y CC se proyecta linealmente sobre cada provincia tomando la distribuci¨®n de sus votos en 2016 como referencia. Con Vox, en cambio, se usan las transferencias desde el resto de partidos hacia la formaci¨®n. Se sabe por encuestas del CIS, Metroscopia e IMOP que alrededor del 60% de los votantes de Vox vienen del PP, un 18% de Cs, un 3% del PSOE, un 4,5% de Podemos y un 15% de la abstenci¨®n. Eso permite estimar su voto en cada provincia a partir del voto de esos partidos en 2016, asumiendo que los flujos son iguales en todas ellas. Esa distribuci¨®n se corrige en Galicia con datos de las encuestas recientes de Sondaxe. Tambi¨¦n se utilizan datos de Sondaxe para proyectar el voto de En Marea, BNG y Podemos en Galicia. En la Comunidad Valenciana, se proyecta el voto de Comprom¨ªs y Unidas Podemos tomando sus resultados de las auton¨®micas de 2015.

Paso 3. Incorporar la incertidumbre de las encuestas. Este es el paso m¨¢s complicado e importante. Se necesita estimar la precisi¨®n esperada de los sondeos. ?De qu¨¦ magnitud son los errores habituales? ?C¨®mo de probable es que se produzcan errores de 2, 3 o 5 puntos? Para responder esas preguntas se estudian cientos de encuestas en Espa?a y miles internacionales.

Calibrar los errores esperados. Primero se estima el error de las encuestas en Espa?a. Se construye una base de datos con todas las elecciones desde 1986. El error absoluto medio (MAE) de los promedios de encuestas ha rondado los 1,9 puntos por partido. Eso significa que fueron habituales desviaciones de 3 o 4 puntos y que el margen de error (al 95%) se acerca a los siete puntos para partidos alrededor del 30% de votos. Esos errores dependen al menos de dos cosas: del tama?o del partido y de la cercan¨ªa de las elecciones. Para tener en cuenta esos dos factores se recurre a la base de datos de Jennings y Wlezien, recientemente publicada en Nature. Se han analizado los errores de m¨¢s de 4.100 encuestas en 241 elecciones de 19 pa¨ªses occidentales. As¨ª se construye un modelo sencillo que estima el error MAE del promedio de votos estimado por las encuestas para cada partido, teniendo en cuenta: i) su tama?o (es m¨¢s f¨¢cil estimar un partido que ronda el 5% en votos que uno que supera el 30%), y ii) los d¨ªas que faltan hasta las elecciones (porque las encuestas mejoran al final).

Elecci¨®n del tipo de distribuci¨®n. Para incorporar la incertidumbre al voto de cada partido en cada simulaci¨®n se utiliza una distribuci¨®n multivariable. Se usan distribuciones t-student en lugar de normales para que tengan colas m¨¢s largas (curtosis): eso hace m¨¢s probable que sucedan eventos muy extremos. Las ventajas de esa hip¨®tesis la explica Nate Silver: "El nivel de curtosis lo he estimado con la base de datos. Luego defino la matriz de covarianzas de estas distribuciones para que la suma de los votos no sobrepase el 100% (una idea de Chris Hanretty). La incertidumbre la incorporo con 53 distribuciones, una a nivel nacional y otra en cada provincia. La primera distribuci¨®n introduce errores iguales para el voto de un partido en toda Espa?a. Es importante hacerlo as¨ª porque en general los errores de las encuestas son sist¨¦micos e iguales en todos los territorios. Si los asumimos independientes, los errores se cancelan entre provincias y el modelo falla por exceso de confianza. Esto pas¨® con algunos modelos de las elecciones de EEUU en 2016. La segunda parte de la incertidumbre la incorporo sobre cada provincia. Por ¨²ltimo, hay que escalar la amplitud de las matrices de covarianza para que las distribuciones de voto que resultan al final tengan el MAE y la desviaci¨®n est¨¢ndar esperados seg¨²n la calibraci¨®n".

Paso 4. Simular. El ¨²ltimo paso consiste en ejecutar el modelo 15.000 veces. Cada iteraci¨®n es una simulaci¨®n de las elecciones con porcentajes de voto que var¨ªan seg¨²n la distribuci¨®n definida en el paso anterior. Los resultados en esas simulaciones permiten calcular las probabilidades que tiene cada partido de lograr cierto n¨²mero de esca?os, alcanzar la mayor¨ªa, quedar primero, etc¨¦tera.

Por qu¨¦ encuestas. Este modelo se basa por entero en encuestas. Existe la percepci¨®n de que los sondeos no son fiables, pero lo cierto es que las encuestas no lo han hecho mal ¨²ltimamente. A nivel nacional fallaron por pocos puntos incluso con Trump o con el Brexit, y desde entonces se han estado bastante precisos en muchas elecciones, como pas¨® en M¨¦xico, Brasil, Colombia, Francia, Pa¨ªses Bajos, Pa¨ªs Vasco, Galicia o Catalu?a. Las encuestas raramente son perfectas, pero no existe ninguna alternativa que se haya demostrado mejor.