El desaf¨ªo matem¨¢tico electoral: ?Qui¨¦n me ha robado mi esca?o?

Con ocasi¨®n de las Elecciones Generales del 10 de noviembre, Ang¨¦lica Benito Sualdea y Adolfo Quir¨®s Graci¨¢n, profesores de Matem¨¢ticas en la Universidad Aut¨®noma de Madrid, nos presentan un nuevo desaf¨ªo electoral propuesto por EL PA?S y la Real Sociedad Matem¨¢tica Espa?ola. En esta ocasi¨®n trata de ver c¨®mo afecta el m¨¦todo de reparto a la asignaci¨®n proporcional de esca?os y, en particular, de si un partido puede o no perder esca?os "enteros". Los lectores pueden enviar sus respuestas hasta las 00.00 del s¨¢bado 9 de noviembre (la medianoche del viernes al s¨¢bado, hora peninsular espa?ola) a problemamatematicas@gmail.com. A continuaci¨®n, para aclarar dudas, a?adimos el enunciado del problema por escrito.

La Constituci¨®n Espa?ola prescribe que en las elecciones al Congreso de los Diputados la asignaci¨®n de esca?os a los partidos debe hacerse en cada circunscripci¨®n con criterios proporcionales. En principio esto no requiere sino una regla de tres: si hay que repartir E esca?os, han votado P personas y p de ellas han optado por un partido, la cantidad de esca?os que le corresponde a ese partido (lo que se llama su cuota) ser¨¢ q= E x p /P. El problema es que, como vemos en el siguiente ejemplo con 3 partidos, 50.000 votantes y 5 esca?os, con lo que es sencillo calcular las cuotas, estas no son siempre n¨²meros enteros:

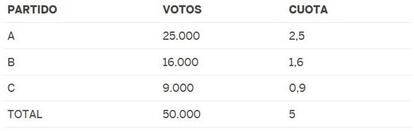
Asignando los esca?os enteros, corresponden 2 al partido A y 1 al B, pero, como no es posible enviar 0,6 diputados de un partido al Congreso, habr¨¢ que decidir a qui¨¦n atribuir los 2 esca?os restantes. Una forma de hacerlo es d¨¢rselos los partidos cuyas cuotas tengan parte decimal m¨¢s grande, en este ejemplo C y B, con lo que el reparto quedar¨ªa as¨ª:

Este procedimiento se conoce como M¨¦todo de los Restos Mayores, y es de hecho lo que nuestra Ley Electoral indica que hay que hacer para establecer cu¨¢ntos esca?os se eligen en cada provincia. Pero para distribuir esca?os entre partidos dentro de una circunscripci¨®n la Ley Electoral dice que debe usarse el M¨¦todo D¡¯Hondt, cuyo funcionamiento recordamos: se dividen los votos de los partidos entre 1, 2, 3,¡­ y los esca?os se asignan sucesivamente a los partidos con los mayores cocientes. En nuestro ejemplo (se?alamos en negrita los cocientes que obtienen esca?os) el resultado ser¨ªa:

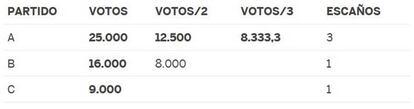
No queremos debatir sobre si este reparto es m¨¢s o menos proporcional que el anterior, porque nuestro objetivo es otro: observar que, aunque podr¨ªa parecer que con el M¨¦todo D¡¯Hondt el partido A le ha ¡°quitado¡± un esca?o al B, en realidad la p¨¦rdida de B respecto a su cuota es solo de 0,6 esca?os, y mantiene el esca?o entero que le correspond¨ªa. No es dif¨ªcil demostrar que el M¨¦todo D¡¯Hondt cumple siempre esta propiedad: asigna a todos los partidos, y en cualquier situaci¨®n, al menos la parte entera de su cuota. No puede por tanto decirse, como se oye a veces, que ¡°D¡¯Hondt quita esca?os a los partidos peque?os para d¨¢rselos a los grandes¡±. La ligera prima que puedan obtener los partidos grandes en una circunscripci¨®n dada viene ¨²nicamente de la atribuci¨®n de partes decimales de esca?os, no de esca?os enteros. (Otra cosa es la ventaja que supone para los partidos grandes que las elecciones al Congreso sean en realidad 52 elecciones separadas, una por circunscripci¨®n, reparti¨¦ndose en la mayor¨ªa de ellas muy pocos esca?os).

Pero hay otros m¨¦todos para repartir esca?os m¨¢s o menos proporcionalmente. Por ejemplo el de Sainte-Lagu?, que se ha propuesto como una posible alternativa para las elecciones al Congreso de los Diputados. Su funcionamiento es similar a D¡¯Hondt, salvo que ahora los votos se dividen s¨®lo entre los n¨²meros impares. Este ser¨ªa el resultado de aplicarlo a nuestro ejemplo:

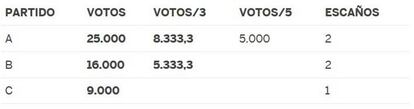
Como se ve, el partido B recupera el esca?o que hab¨ªa ¡°perdido¡± con D¡¯Hondt. Quiz¨¢s resulte sorprendente que no todos los m¨¦todos de reparto compartan con D¡¯Hondt la propiedad natural de que, en cualquier situaci¨®n, ning¨²n partido pierda esca?os ¡°enteros¡±. En particular, el M¨¦todo de Sainte-Lagu? puede en algunos casos (no sucede en nuestro ejemplo) asignar a un partido menos esca?os de los que indica la parte entera de su cuota.

El desaf¨ªo que proponemos a nuestros lectores es que nos presenten un ejemplo en el que se d¨¦ esta situaci¨®n: hay un partido al que el M¨¦todo de Sainte-Lagu? no le asigna todos los esca?os enteros que le corresponder¨ªan atendiendo a su cuota.

Quienes se animen son libres de elegir el n¨²mero de esca?os a repartir, el de partidos, el total de votantes y cu¨¢ntos deciden votar a cada partido. Esperamos que den tambi¨¦n una breve indicaci¨®n de c¨®mo han llegado al ejemplo. Esperamos vuestras respuestas.