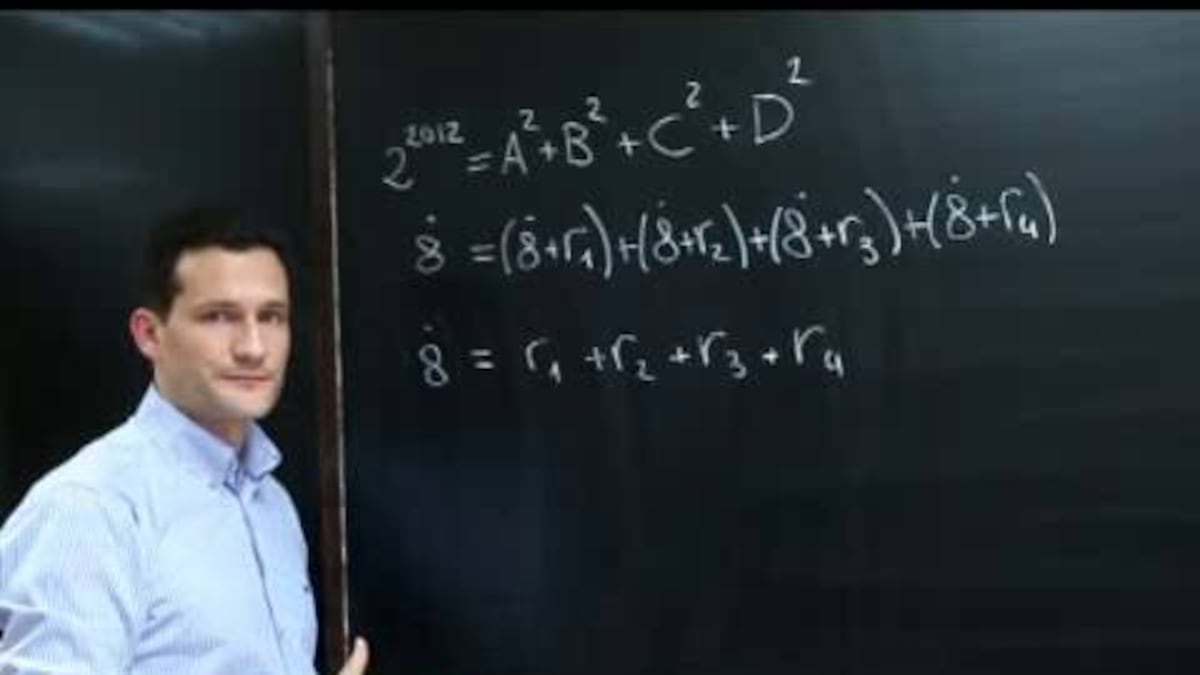Una ¨²nica suma posible de cuadrados

Ya hay soluci¨®n para el decimonoveno desaf¨ªo matem¨¢tico con el que EL PA?S celebra el centenario de la Real Sociedad Matem¨¢tica Espa?ola (ver el v¨ªdeo conmemorativo). Juan Gonz¨¢lez-Meneses, Profesor Titular de la Universidad de Sevilla propuso el problema (ver v¨ªdeo de la izquierda) y lo resuelve ahora (v¨ªdeo de la derecha): hay una manera de descomponer 2^2012 como suma de cuatro cuadrados, y ninguna manera de descomponer 2^2011. El ganador de una biblioteca matem¨¢tica como la que entrega cada semana EL PA?S ha sido en esta ocasi¨®n Iago Vaamonde Paniagua, estudiante de Ingenier¨ªa Industrial, de Vigo. Este domingo, en el quiosco, por 9,95 euros con el peri¨®dico, Hipotecas y ecuaciones. Las matem¨¢ticas de la econom¨ªa, de Llu¨ªs Artal y Josep Sales.

Esta semana se han recibido 320 respuestas, de las que un 50% daban la respuesta correcta. De las respuestas correctas, aproximadamente la mitad usaban un razonamiento similar a la soluci¨®n propuesta en el v¨ªdeo, y el resto hac¨ªa uso del Teorema de Jacobi, que da el n¨²mero de formas de escribir un n¨²mero natural como suma de cuatro cuadrados... de n¨²meros enteros (incluyendo el cero, y contando como soluciones distintas las que se obtienen al cambiar de orden los sumandos).

Algunas respuestas calculaban la descomposici¨®n de peque?as potencias de 2, y daban por supuesto que para potencias de 2 m¨¢s grandes se segu¨ªa el mismo patr¨®n. Aunque esto sea cierto, la simple observaci¨®n de los primeros casos no garantiza que la misma propiedad sea cierta para potencias de 2 mayores. Por tanto, este tipo de respuestas no se puede considerar como v¨¢lida.

Recordemos el problema: queremos saber de cu¨¢ntas formas se puede descomponer 2^2012 (y tambi¨¦n 2^2011) como suma de cuatro cuadrados perfectos de n¨²meros naturales (sin incluir el cero).

La soluci¨®n propuesta por el Profesor Gonz¨¢lez-Meneses es la siguiente:

Supongamos que tenemos una forma de escribir 2^2012 como suma de cuatro cuadrados: 2^2012=A^2+B^2+C^2+D^2. Para obtener informaci¨®n sobre estos cuatro n¨²meros A, B, C y D, usaremos un m¨¦todo muy ¨²til para trabajar con n¨²meros grandes: miraremos los restos que se obtienen al dividir cada sumando por un n¨²mero peque?o, en este caso, el 8.

Veamos cu¨¢l es el resto de dividir A^2 entre 8.

Si A es par (m¨²ltiplo de 2), su cuadrado ser¨¢ m¨²ltiplo de 4. Por tanto, el resto de dividir A^2 entre 8, en este caso, debe ser 0 o 4.

Si A es impar, se escribir¨¢ A=2k+1. Su cuadrado ser¨¢ A^2=4k^2+4k+1=4k(k+1)+1. Observemos que, o bien k, o bien k+1 debe ser par, luego 4k(k+1) es m¨²ltiplo de 8. Por tanto, el resto de dividir A^2 entre 8, en este caso, es 1.

An¨¢logamente, el resto de dividir B^2, C^2 o D^2 entre 8 debe ser tambi¨¦n 0, 1 o 4.

Como la suma de los cuatro cuadrados es igual a 2^2012, que es m¨²ltiplo de 8, los cuatro restos deben sumar obligatoriamente 0, 8 o 16. Y como los restos s¨®lo pueden ser 0, 1 o 4, se observa f¨¢cilmente (por ejemplo haciendo todas las combinaciones posibles), que nunca puede haber un 1. Es decir, A, B, C y D deben ser pares, y podremos escribirlos A=2a, B=2b, C=2c y D=2d.

Pero entonces, si tomamos la igualdad 2^2012=A^2+B^2+C^2+D^2 y la dividimos entre 4, obtenemos 2^2010=a^2+b^2+c^2+d^2. Podemos ahora repetir el argumento, concluyendo que a, b, c y d son pares, lo que nos da una descomposici¨®n como suma de cuatro cuadrados de 2^2008, luego otra de 2^2006, 2^2004, etc, dividiendo cada vez por 4 la igualdad anterior. Esto nos llevar¨ªa a obtener una descomposici¨®n de 2^2=4 como suma de cuatro cuadrados. Pero la ¨²nica descomposici¨®n posible es 4=1+1+1+1, que s¨®lo puede provenir de 2^2012=2^2010+2^2010+2^2010+2^2010. Es decir, 2^2012=(2^1005)^2+(2^1005)^2+(2^1005)^2+(2^1005)^2 es la ¨²nica forma de descomponer 2^2012 como suma de cuatro cuadrados.

En el caso de 2^2011, el mismo argumento nos dice que cualquier descomposici¨®n de 2^2011 como suma de cuatro cuadrados, nos dar¨ªa otra de 2^2009, 2^2007, etc. hasta llegar a 2^1=2. Pero como 2 no se puede descomponer como suma de cuatro cuadrados, se deduce que no hay ninguna manera de descomponer 2^2011 como suma de cuatro cuadrados.

Muchos participantes han usado un argumento similar, variando ligeramente la forma de demostrar que los cuatro sumandos son cuadrados de n¨²meros pares. La otra soluci¨®n m¨¢s habitual consiste en utilizar un teorema de Carl Gustav Jakov Jacobi. Jacobi demostr¨® que el n¨²mero de cuaternas (A,B,C,D) de n¨²meros enteros, tales de n=A^2+B^2+C^2+D^2 es igual a 8 veces la suma de los divisores de n, si n es impar, y 24 veces la suma de los divisores impares de n, si n es par. En nuestro caso, como 2^2012 y 2^2011 son pares, y su ¨²nico divisor impar es 1, el teorema de Jacobi nos dice que hay exactamente 24 cuaternas posibles.

De esas cuaternas hay que descartar las que contengan al cero o a un entero negativo, e identificar las que se obtengan al cambiar de orden los cuatro n¨²meros. La mayor¨ªa de los participantes han encontrado las 24 posibles cuaternas, y han deducido la respuesta correcta de esta forma.

Aunque tambi¨¦n se puede deducir el resultado sin "adivinar" las 24 cuaternas, como propone Rafael Haro: Buscamos cuaternas de n¨²meros mayores que cero. Si hubiera alguna en que dichos n¨²meros no fueran todos iguales, alguna permutaci¨®n de esos n¨²meros dar¨ªa una cuaterna distinta, y todas las posibilidades de cambio de signo (16 por cada cuaterna), nos dar¨ªan como m¨ªnimo 32 cuaternas diferentes. Esto contradice el teorema de Jacobi, por tanto los cuatro n¨²meros deben ser iguales. De ah¨ª se deduce inmediatamente la ¨²nica descomposici¨®n posible de 2^2012, y que no existe ninguna para 2^2011.

El inconveniente de usar el teorema de Jacobi puede ser en alg¨²n caso que nos quedemos con la sensaci¨®n de que la respuesta es as¨ª "porque lo dice Jacobi", pero no que uno haya conseguido hacer suya la soluci¨®n. De hecho hay un cierto riesgo de, c¨®mo les ha sucedido a algunos lectores, no ser capaz de llegar del resultado de Jacobi a la respuesta correcta al desaf¨ªo. Pero no cabe duda de que muchos han hecho bien el tr¨¢nsito.

Otros lectores han deso¨ªdo en parte nuestro consejo de no usar ordenadores. Pero no los han empleado para "calcular todas las posibilidades" (ya se?alamos que eran demasiadas), sino para encontrar una pauta y conjeturar cu¨¢l era la soluci¨®n. Y luego lo han demostrado. Nada que objetar a ese procedimiento, m¨¢s bien al contrario.

El viernes -ojo, cambiamos el d¨ªa de la semana- plantearemos ?atenci¨®n! cinco desaf¨ªos: el correspondiente al ¨²ltimo fin de semana de julio y todos los de agosto. As¨ª que esta vez los lectores tendr¨¢n cinco semanas enteras para resolver los retos, planteados por quintuplicado eso s¨ª. Naturalmente habr¨¢ cinco premios -cinco bibliotecas matem¨¢ticas- y sortearemos una entre los acertantes de cada problema.

Una ¨²nica suma posible

Cuadrados que suman grandes cifras