La complejidad matem¨¢tica del ¡°juego de la vida¡±
Lo que empez¨® siendo un sencillo entretenimiento matem¨¢tico ha llevado su aplicaci¨®n como simulaci¨®n de procesos f¨ªsicos y biol¨®gicos
Reglas muy sencillas pueden dar lugar a comportamientos muy complejos. Si hubiera que resumir el juego de la vida (Game of Life o, simplemente Life) en una frase, esta ser¨ªa su mejor descripci¨®n. Algo que describe lo que sucede cuando se aplica un sencillo conjunto de reglas a uno de los aut¨®matas celulares m¨¢s simples que se conocen. D¨¦cadas despu¨¦s todav¨ªa se sigue examinando hasta donde llega esa complejidad, y cu¨¢les son las aplicaciones pr¨¢cticas de esta construcci¨®n matem¨¢tica y de otras similares.
Un juego que es m¨¢s que un juego
Para explicar en qu¨¦ consiste este peculiar juego surgido del mundo de la computaci¨®n te¨®rica primero hay que describir lo que es un aut¨®mata celular. En palabras sencillas es un modelo matem¨¢tico que cambia paso a paso. Suele tener el aspecto de un tablero infinito, normalmente, de celdas cuadradas. Y el transcurrir del tiempo lo marca una especie de reloj universal.
Con cada tic se aplican unas reglas predefinidas a las "c¨¦lulas" y se toma una decisi¨®n sobre lo que sucede individualmente con cada una de ellas. Las celdas m¨¢s simples solo tienen dos estados: apagadas o encendidas. Cuando se ha completado el c¨¢lculo de todo lo que sucede en tan cuadriculado universo la operaci¨®n comienza de nuevo.
Todo esto puede tener lugar en un escenario geom¨¦trico con diversos patrones (tri¨¢ngulos, hex¨¢gonos) e incluso en m¨¢s o menos de dos dimensiones: hay aut¨®matas de una sola dimensi¨®n (celdas en l¨ªnea), 3D (cubos), 4D y otras dimensiones. Sus estados tambi¨¦n pueden ser m¨¢s complejos que una simple matriz de p¨ªxeles blancos y negros. Los hay con tres, cuatro o m¨¢s estados, simbolizados normalmente por colores. Lo mismo sucede con las reglas: normalmente a cada celda solo le afecta las inmediatamente adyacentes, pero se pueden inventar reglas otras m¨¢s complicadas e incluso acciones a distancia.
El pionero de la computaci¨®n John von Neumann fue el primero en llamar la atenci¨®n en la d¨¦cada de los 50 sobre los aut¨®matas celulares a modo de curiosas construcciones imaginarias como parte de sus ideas sobre la autorreplicaci¨®n en computaci¨®n.
Lo verdaderamente interesante est¨¢ en lo que sucede en los aut¨®matas m¨¢s sencillos. Porque complejidad puede a?adirla cualquiera, pero en un simple escenario de p¨ªxeles cuadrados en blanco y negro, con un pu?ado de reglas minimalistas, ?qu¨¦ puede surgir? El matem¨¢tico John H. Conway experiment¨® con ellos ¨Ccon l¨¢piz y papel, al igual que von Neumann¨C y hall¨® en 1970 unas sencillas y prometedoras reglas que generaban comportamientos interesantes. Llam¨® a su descubrimiento el juego de la vida y las celdas pasaron a llamarse c¨¦lulas.
Seg¨²n estas reglas en cada paso se examina cada c¨¦lula y sus ocho vecinas y se toma una de estas decisiones: (1) Si la c¨¦lula est¨¢ rodeada por menos de otras dos c¨¦lulas, muere. (2) Si est¨¢ junto a 2 o 3 c¨¦lulas vecinas, sigue viviendo. (3) Si est¨¢ rodeada por m¨¢s de tres, tambi¨¦n muere. (4) Si en una celda vac¨ªa hay exactamente tres c¨¦lulas a su alrededor, nace una nueva c¨¦lula. Es f¨¢cil hacer pruebas con l¨¢piz y papel dibujando algunas c¨¦lulas y calculando lo que suceder¨¢ a cada paso. A veces todas las c¨¦lulas mueren, a veces entran en bucle, a veces dibujan curiosos patrones y otras parecen expandirse sin fin. As¨ª empez¨® Conway y luego una multitud sigui¨® sus pasos.
Ampliando las reglas
El mismo a?o en que Conway descubri¨® su juego el divulgador Martin Gardner publicaba acerca de ¨¦l en su columna de la revista Scientific American, llegando a un mont¨®n de aficionados a las matem¨¢ticas recreativas que tambi¨¦n se iniciaban en la era de los ordenadores personales. Programar el juego era sencillo y muchos se pusieron a experimentar con fruici¨®n, creando animaciones, buscando patrones y objetos de comportamiento curioso. Era bonito ver c¨®mo progresaban. Y llamativa toda la vida que casi literalmente surg¨ªa de un juego y unas reglas tan simples. (Para quien quiera probarlo en la web muchos simuladores, por ejemplo Game of Life, de Edwin Martin y JavaScript Game of Life de Pedrovam).
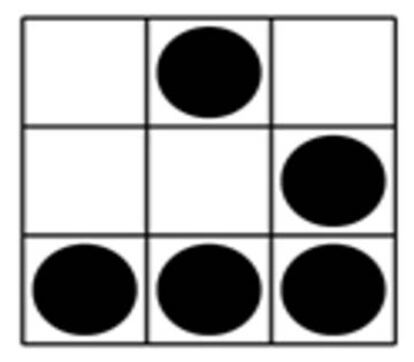
Entre otras cosas se descubrieron objetos que se mov¨ªan sin fin (los glider, que se tradujeron como deslizadores o planeadores), grandes estructuras complejas que interactuaban unas con otras y diversas rarezas ¨C todo idealmente visualizado en los p¨ªxeles cuadrados de las pantallas del ordenador. No es casualidad que el emblema hacker sea precisamente uno de esos deslizadores, unificando as¨ª la cultura de la computaci¨®n con las matem¨¢ticas y el esp¨ªritu apasionado y creativo de la investigaci¨®n.
Con la llegada de ordenadores m¨¢s potentes y software m¨¢s avanzado se utiliz¨® el juego de la vida para crear puertas l¨®gicas como las de los microprocesadores. Pudiendo combinarlas a gran escala las estructuras del juego eran capaces de simular la electr¨®nica de un circuito ¨Cde forma terriblemente lenta, eso s¨ª¨C , pero ah¨ª estaban los resultados. Se ingeniaron m¨®dulos acoplables con diversas funciones, como conversores en forma de d¨ªgitos visibles y otras maravillas. Y finalmente se construy¨® una m¨¢quina universal de Turing, un artefacto te¨®rico que si contara con memoria infinita y tiempo tambi¨¦n infinito podr¨ªa realizar cualquier computaci¨®n posible ¨C incluyendo emular a otros ordenadores. Windows 10 a partir de las c¨¦lulas que se encienden y apagan, en otras palabras.
M¨¢s all¨¢ de las simulaciones
Otro de los personajes que m¨¢s ha investigado en las ¨²ltimas d¨¦cadas los aut¨®matas celulares es el f¨ªsico Stephen Wolfram. Joven prodigio y creador del software Mathematica dedic¨® su sesudo y controvertido libro A New Kind Science a explicar los resultados de su exploraci¨®n. Comenz¨® como von Neumann y Conway, con l¨¢piz, papel y ordenadores primitivos, pero decidi¨® revisar todas las posibilidades de los aut¨®matas celulares de forma emp¨ªrica y exhaustiva, uno por uno. As¨ª que prob¨® todo lo que se pod¨ªa probar en cuanto a definiciones y reglas de estos peculiares sistemas. Los clasific¨®, numer¨® y defini¨® los que exhib¨ªan un comportamiento que calific¨® como de "interesante".
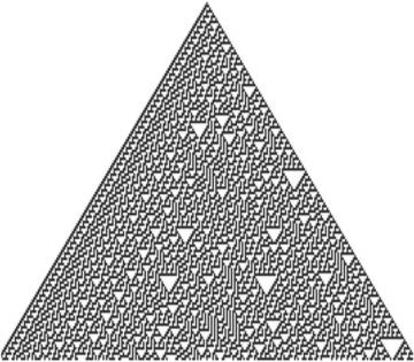
Esto le llev¨® a concluir que hay programas muy simples pueden generar comportamientos muy complejos, pr¨¢cticamente como los sistemas ca¨®ticos, y que hay muchas similitudes entre el funcionamiento de los aut¨®matas celulares con el de las leyes f¨ªsicas del universo. Examinando sus aut¨®matas (algunos de los cuales tienen simplemente un n¨²mero de orden, como Regla 30 o Regla 110) se pueden apreciar similitudes con la termodin¨¢mica y otros fen¨®menos y estructuras del universo, incluyendo las part¨ªculas subat¨®micas. Uno de sus aut¨®matas incluso se patent¨® como generador de n¨²meros aleatorios ¨C dado lo impredecible que resultaba. ?Todo eso surgido de unas reglas extremadamente simples? As¨ª era.
En esa b¨²squeda Wolfram tambi¨¦n descubri¨® algunos aut¨®matas que resultaron ser m¨¢quinas universales de Turing. Aplicando lo que define como "principio de equivalencia computacional" plantea desde un punto de vista te¨®rico y filos¨®fico que quiz¨¢ vivimos en un universo computable. Ninguna de estas ideas es exactamente nueva, y muchas de hecho ya hab¨ªan sido examinadas con anterioridad por diversos autores, mientras que otras est¨¢n todav¨ªa abiertas o son cuestionadas por otros cient¨ªficos, pero su trabajo al respecto es digno de menci¨®n.
Aplicaciones pr¨¢cticas
Mientras tanto, los aut¨®matas celulares se han hecho un hueco en otras ¨¢reas. Una de las aplicaciones pr¨¢cticas es servir como base para simulaciones f¨ªsicas a partir de unas reglas o premisas extremadamente simples. Un ejemplo es el simulador de l¨ªquidos en dos dimensiones que permite ver algunas de sus posibilidades. Las reglas son muy parecidas a las del juego de la vida y hacen comportarse a los p¨ªxeles de distintos colores como ¨¢tomos sobre los que act¨²an fuerzas como la presi¨®n y la gravedad.
Entre otras aplicaciones tambi¨¦n est¨¢n las simulaciones de ciertos procesos qu¨ªmicos o incluso biol¨®gicos, tales como la formaci¨®n de los patrones en la piel, el pelo o las conchas de ciertos animales. En las plantas sucede otro tanto: el comportamiento de los estomas (c¨¦lulas de la epidermis de las hojas) es relativamente f¨¢cil de simular con unas pocas reglas. Con algo m¨¢s de complejidad se puede simular tambi¨¦n el funcionamiento de las neuronas, creando modelos que pese a su simplicidad acaban mostrando una extraordinaria complejidad cuando se les aplican ciertos patrones o valores iniciales.
En el fondo, esa es la grandeza del comportamiento tanto del juego de la vida como de otros aut¨®matas celulares: que de algo tan simple pueda surgir algo elaborado y complejo. Tan elaborado y tan complejo que todav¨ªa hoy en d¨ªa se siguen estudiando.
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
