Las herramientas matem¨¢ticas que han revolucionado la tecnolog¨ªa digital

En su edici¨®n de 2020, el Premio Princesa de Asturias de Investigaci¨®n Cient¨ªfica y T¨¦cnica ha sido concedido a cuatro matem¨¢ticos: Yves Meyer (ENS Par¨ªs Saclay), Ingrid Daubechies (Universidad de Duke), Terence Tao (UCLA) y Emmanuel Cand¨¨s (Universidad de Stanford). El jurado reconoce sus contribuciones pioneras y trascendentales a las teor¨ªas y t¨¦cnicas matem¨¢ticas para el procesamiento de datos, que han ampliado extraordinariamente la capacidad de observaci¨®n de nuestros sentidos y son base y soporte de la moderna era digital. ?De qu¨¦ tratan estas aportaciones? Y ?c¨®mo han llegado a revolucionar nuestro mundo digital?

Yves Meyer e Ingrid Daubechies trabajaron, en la d¨¦cada de los 80, en el desarrollo de la moderna teor¨ªa matem¨¢tica de las ond¨ªculas. Podemos imaginar estos objetos abstractos como ¨¢tomos que, convenientemente unidos, representan los sonidos y las im¨¢genes, de un modo que permite comprimirlos sin casi p¨¦rdida de calidad o eliminar el ruido que ha aparecido durante su obtenci¨®n.

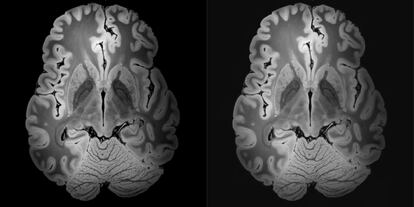
Las ond¨ªculas se emplean en multitud de escenarios, uno de ellos es el procesado de im¨¢genes m¨¦dicas. Por ejemplo, para comprimir (y as¨ª guardar o enviar de forma eficiente) im¨¢genes de capas cerebrales, sin perder informaci¨®n relevante. Lo m¨¢s importante de estas im¨¢genes son los bordes que delimitan las distintas zonas, y las ond¨ªculas permiten detectarlos de manera eficiente, guardar ¨¦sta informaci¨®n y desechar el resto. El resultado es una imagen de mucho menor tama?o, pero visualmente similar a la original.

Dise?ar esta vers¨¢til herramienta matem¨¢tica no fue sencillo. En 1984 Ives Meyer, inspirado por investigaciones realizadas sobre prospecciones petrol¨ªferas, y empleando su profundo conocimiento del an¨¢lisis arm¨®nico, ide¨® las primeras ond¨ªculas, no especialmente aptas para el procesamiento de im¨¢genes. Tres a?os m¨¢s tarde, en colaboraci¨®n con St¨¦phane Mallat (Coll¨¨ge de France), cre¨® el an¨¢lisis multirresoluci¨®n (AMR), una herramienta matem¨¢tica basada en principios ¨®pticos, que permite construir ond¨ªculas a partir de una part¨ªcula a¨²n m¨¢s elemental. Esta t¨¦cnica fue la usada por Ingrid Daubechies en 1988 para dise?ar las ond¨ªculas con soporte compacto, una de cuyas variantes es la base del algoritmo est¨¢ndar de compresi¨®n de im¨¢genes digitales, llamado JPEG2000.

Diversos tipos de waveletes tambi¨¦n se usan para eliminar el ruido que se puede producir al escuchar un sonido, y han sido clave en la detecci¨®n de las ondas gravitacionales producidas por la colisi¨®n de dos agujeros negros lograda recientemente con el experimento LIGO, entre muchas otras aplicaciones.

Por otro lado, ya a comienzos del siglo XXI, Terence Tao y Emmanuel Cand¨¨s colaboraron en la creaci¨®n de la t¨¦cnica de percepci¨®n comprimida (compressed sensing, en ingl¨¦s), que posibilita la reconstrucci¨®n de una imagen con pocas mediciones. Esto permite, entre otras aplicaciones, reducir el tiempo que se tarda en realizar un esc¨¢ner sin perder la calidad de la imagen obtenida.

Para obtener im¨¢genes m¨¦dicas de calidad con mediciones efectuadas con resonancia magn¨¦tica (MRI) es necesario efectuar muchas medidas, cambiando la direcci¨®n del campo magn¨¦tico, mientras que el paciente deber¨ªa de permanecer inm¨®vil. Esto, en la pr¨¢ctica, limita el n¨²mero de mediciones, lo que provoca que la informaci¨®n disponible sea insuficiente para poder reconstruir adecuadamente la imagen deseada con la teor¨ªa cl¨¢sica del an¨¢lisis de Fourier. Es como si quisi¨¦ramos averiguar cu¨¢nto ha pagado cada comensal de una misma mesa conociendo solo el total de la cuenta.

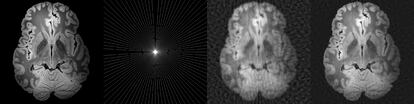
Es aqu¨ª donde entra la percepci¨®n comprimida, que permite encontrar soluciones tanto a este como a muchos otros problemas indeterminados de reconstrucci¨®n de datos. La idea de Cand¨¨s y Tao se basa en el principio de buscar, entre todas las soluciones posibles, la menos compleja. Su contribuci¨®n fundamental fue encontrar las dos condiciones que permiten garantizar que esta soluci¨®n casi siempre se acerca mucho a la correcta. La primera condici¨®n es que los datos sean dispersos. Esto significa que existe alg¨²n diccionario que permite representarlos con pocas palabras. En el caso de las im¨¢genes, esto equivaldr¨ªa a la compresi¨®n dada por las ond¨ªculas. La segunda es que las mediciones, est¨¦n lo menor relacionadas posible con este diccionario. Adem¨¢s, Cand¨¦s y Tao fueron capaces de definir c¨®mo tienen que ser estas mediciones ?sin conocer el diccionario!

Todos estos trabajos, reconocidos ahora por uno de los premios cient¨ªficos de m¨¢s prestigio en nuestro pa¨ªs, muestran la importancia de las matem¨¢ticas en el desarrollo de procesos que son b¨¢sicos en la tecnolog¨ªa actual.

Davide Barbieri es profesor ayudante doctor en la Universidad Aut¨®noma de Madrid (UAM) y miembro del Instituto de Ciencias Matem¨¢ticas (ICMAT), y Eugenio Hern¨¢ndez es profesor titular de la UAM.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n Garc¨ªa-Longoria (ICMAT)

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter