Teselados pentagonales

Ve¨ªamos la semana pasada que los ocho tipos de teselados semirregulares responden a la notaci¨®n:

3.3.3.3.6, 3.3.3.4.4, 3.3.4.3.4, 3.4.6.4, 3.6.3.6, 3.12.12, 4.6.12, 4.8.8

Los n¨²meros separados por puntos indican el n¨²mero de lados de cada uno de los pol¨ªgonos regulares que confluyen en un v¨¦rtice, empezando por los de menos lados y en sentido giratorio. As¨ª, 3.4.6.4 significa que en cada v¨¦rtice del teselado confluyen un tri¨¢ngulo equil¨¢tero, dos cuadrados y un hex¨¢gono regular, en el orden tri¨¢ngulo-cuadrado-hex¨¢gono cuadrado, tal como se ve en la figura.

La notaci¨®n no indica el tama?o relativo de los pol¨ªgonos regulares implicados; pero es que para cada combinaci¨®n solo hay una correlaci¨®n de tama?os posible.

En cuanto a la posibilidad de teselar el plano con cualquier cuadril¨¢tero y con algunos hex¨¢gonos irregulares, nuestro comentarista habitual Luca Tanganelli ha enviado la siguiente reflexi¨®n (ilustrada):

¡°Los cuadril¨¢teros se dividen en tri¨¢ngulos que teselan el plano en ¡°tiras¡± (l¨ªneas discontinuas). Adem¨¢s, se revela un segundo teselado con hex¨¢gonos que se obtienen duplicando por simetr¨ªa rotacional cada cuadril¨¢tero (en rojo). Por lo tanto, que un hex¨¢gono se pueda dividir en dos cuadril¨¢teros iguales es condici¨®n suficiente para teselar el plano (un hex¨¢gono c¨®ncavo tambi¨¦n puede teselar); pero si es necesaria no lo s¨¦ a¨²n¡±.

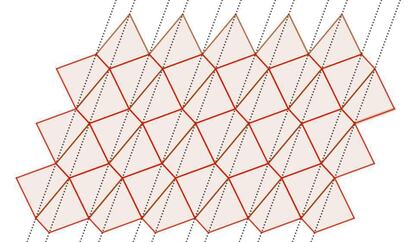
?Es condici¨®n necesaria, para que un hex¨¢gono pueda teselar el plano, que pueda dividirse en dos cuadril¨¢teros iguales? Otros¨ª: ?De qu¨¦ otra manera se puede formular la condici¨®n necesaria y suficiente?

Teselados pentagonales monoedrales convexos

Es evidente que no se puede teselar el plano con pent¨¢gonos regulares, puesto que el ¨¢ngulo interior de un pent¨¢gono regular mide 108?, que no es divisor de 360? (s¨ª que pueden, sin embargo, los pent¨¢gonos regulares recubrir una superficie esf¨¦rica o hiperb¨®lica).

Con algunos pent¨¢gonos irregulares es posible teselar el plano, como vimos al hablar del mosaico de El Cairo, el m¨¢s conocido ejemplo de recubrimiento de una superficie plana mediante piezas pentagonales convexas de la misma forma y tama?o: lo que t¨¦cnicamente se denomina un teselado pentagonal monoedral convexo.

A lo largo del siglo XX y lo que va del XXI, se han descubierto 15 tipos distintos de estos teselados (el ¨²ltimo en fecha tan reciente como 2015), y parece ser que no hay m¨¢s posibilidades (hay una demostraci¨®n de imposibilidad pendiente de comprobaci¨®n, aunque es probable que en el momento de escribir estas l¨ªneas ya haya sido comprobada). No es sorprendente que Martin Gardner y su secci¨®n de juegos matem¨¢ticos de Scientific American desempe?aran un papel importante en esta investigaci¨®n; pero s¨ª lo es que una matem¨¢tica aficionada sin ninguna formaci¨®n universitaria descubriera 4 de los 15 teselados pentagonales monoedrales convexos posibles: es el extraordinario caso de la recientemente fallecida Marjorie Rice (1923-2017), que incluso cre¨® su propia forma de notaci¨®n operativa y su personal l¨ªnea de trabajo (desarrollada, como ella misma cont¨®, en la cocina de su casa), y cuya web Intriguing Tessellations merece una visita de mis sagaces lectoras/es.

En la imagen, los 4 tipos de teselado pentagonal descubiertos por Rice, que demostr¨® que un matem¨¢tico aficionado -y una matem¨¢tica aficionada- a¨²n puede hacer aportaciones al m¨¢s alto nivel.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.