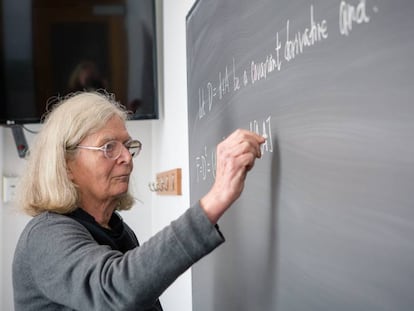Cuatro matem¨¢ticos demuestran que era imposible predecir el destino de 29.000 patitos de goma en el mar

El mar se llen¨® de patitos amarillos, tortugas azules, ranas verdes y castores rojos el 10 de enero de 1992. A un buque carguero se le cay¨® por la borda un contenedor con 29.000 juguetes de pl¨¢stico para la ba?era durante una violenta tormenta en el Pac¨ªfico Norte, justo a medio camino entre Asia y Am¨¦rica. Siete meses despu¨¦s del accidente, se empezaron a encontrar cientos de mu?ecos de goma en la costa de Sitka, en Alaska, no muy lejos de otro vertido de 61.000 zapatillas Nike ocurrido dos a?os antes. Al ocean¨®grafo estadounidense Curtis Ebbesmeyer se le ocurri¨® entonces estar atento durante a?os a los avistamientos de aquellos objetos a la deriva, con el objetivo de aprender a predecir las corrientes marinas. Cuatro matem¨¢ticos espa?oles, enfrent¨¢ndose a otro problema monumental, han resuelto de rebote el enigma de los patitos de goma flotando en el Pac¨ªfico: era imposible predecir en qu¨¦ playa aparecer¨ªan. Parece un divertimento, pero la investigaci¨®n se publica en una de las mejores revistas cient¨ªficas del mundo, PNAS, por sus potenciales implicaciones para la humanidad.

Una fundaci¨®n estadounidense, el Instituto Clay de Matem¨¢ticas, anunci¨® en el a?o 2000 que entregar¨ªa un mill¨®n de d¨®lares a quien resolviera cualquiera de los llamados ¡°siete problemas del milenio¡±, enigmas matem¨¢ticos endiabladamente complejos. Uno de ellos tiene que ver con las ecuaciones de Navier-Stokes, que describen el movimiento de los l¨ªquidos y los gases. Fueron formuladas entre 1821 y 1845 por el matem¨¢tico franc¨¦s Claude-Louis Navier y por el f¨ªsico irland¨¦s George Stokes. Teniendo en cuenta factores como la temperatura, la viscosidad y la velocidad inicial de un fluido, las ecuaciones calculan su velocidad en un momento posterior. Casi 200 a?os despu¨¦s de su planteamiento, se desconoce si las soluciones a estas f¨®rmulas tienen siempre una cierta regularidad o pueden tener una explosi¨®n, un cambio brusco de comportamiento. Averiguarlo vale un mill¨®n de d¨®lares.

La matem¨¢tica Eva Miranda cuenta que iba aburrida en el tren Madrid-Barcelona un d¨ªa de febrero de 2019 cuando, ojeando la red social Twitter, se enter¨® de que el investigador australiano Terence Tao hab¨ªa publicado en su blog los ¨²ltimos detalles de su batalla para resolver ese problema del milenio. Tao fue un ni?o prodigio de las matem¨¢ticas. Con 14 a?os empez¨® su grado universitario de Ciencia. Con 20 a?os ya se hab¨ªa doctorado en matem¨¢ticas en la Universidad de Princeton (EE UU). Con 31 a?os recibi¨® la medalla Fields, uno de los premios m¨¢s prestigiosos de la disciplina. Y ahora, con 45 a?os, todav¨ªa le llaman ¡°el Mozart de las matem¨¢ticas¡±.

Tao anunci¨® en 2014 que pretende simular de manera abstracta una especie de ordenador hecho con agua, para forzar al l¨ªquido a que acumule energ¨ªa hasta que se detecte un cambio brusco con las ecuaciones de Navier-Stokes. A Miranda, catedr¨¢tica de la Universidad Polit¨¦cnica de Catalu?a nacida en Reus (Tarragona) hace 47 a?os, se le encendi¨® la bombilla en el tren y llam¨® a tres colegas para proponerles una idea.

Los cuatro matem¨¢ticos ¡ªRobert Cardona, Eva Miranda, Daniel Peralta y Francisco Presas¡ª anunciaron este mi¨¦rcoles que han conseguido dise?ar una m¨¢quina abstracta de agua por primera vez. Los investigadores se han basado en una m¨¢quina de Turing, un dispositivo que recibe una secuencia de n¨²meros con un c¨®digo binario, unos y ceros, y genera un resultado, tambi¨¦n expresado en unos y ceros, tras aplicar unas determinadas reglas. La m¨¢quina de agua de los cuatro matem¨¢ticos toma como dato de entrada un punto del espacio y ofrece como resultado el punto al que se ha desplazado el fluido.

Miranda explica que su m¨¢quina permite demostrar que el comportamiento turbulento de los fluidos es un problema ¡°indecidible¡±: las matem¨¢ticas se quedan cortas para resolverlo. No es que los matem¨¢ticos sean torpes ni tiene nada que ver con la famosa impredecibilidad de la teor¨ªa del caos (el aleteo de una mariposa genera un tornado), es que ning¨²n algoritmo permite afirmar que un fluido pasar¨¢ por un punto en un tiempo determinado. ¡°Somos los primeros en demostrar que no puedes encontrar los patitos de goma, suponiendo que se mueven en tres dimensiones¡±, recalca Miranda. ¡°Es como si lanzo al mar un mensaje de amor en una botella. Seguir¨¢ una trayectoria y al cabo de un tiempo estar¨¢ en otro sitio. Lo que hemos demostrado es que no podemos predecir d¨®nde estar¨¢, as¨ª que es mejor mandar un wasap¡±, bromea la matem¨¢tica.

Algunos juguetes de goma del accidente de 1992 aparecieron a?os o incluso d¨¦cadas despu¨¦s en las costas de medio mundo, seg¨²n mostr¨® la BBC en su serie documental Planeta Azul 2. Unos llegaron a Alaska, otros a Australia, otros a Jap¨®n y algunos incluso atravesaron el ?rtico y pasaron del oc¨¦ano Pac¨ªfico al Atl¨¢ntico. Eva Miranda recuerda que, poco antes del vertido de patitos, el f¨ªsico estadounidense Cris Moore ya se pregunt¨® si los fluidos son lo suficientemente complejos como para hacer todas las posibles operaciones de un ordenador. ¡°Nosotros demostramos que s¨ª¡±, sentencia Miranda.

Terence Tao aplaude el trabajo de sus cuatro colegas espa?oles. ¡°M¨¢s que la soluci¨®n, es una evidencia de la dificultad del problema [del mill¨®n de d¨®lares]¡±, explica a EL PA?S. La nueva m¨¢quina de agua no se aplica al espacio tridimensional plano en el que vivimos, sino a una versi¨®n curva simplificada, matiza Tao. ¡°Pero s¨ª muestra que los fluidos pueden volverse tan complejos en esos espacios curvos que, en cierto modo, pueden comportarse como una computadora, de manera que puedes programar un fluido para hacer cualquier cosa que se pueda programar en una computadora¡±, explica el investigador australiano, de la Universidad de California en Los ?ngeles. ¡°Creo que el mismo tipo de fen¨®meno tambi¨¦n ocurre en nuestro mundo plano tridimensional, lo que descartar¨ªa muchos tipos de enfoques para resolver el problema de la regularidad de las ecuaciones de Navier-Stokes, que se basan en mostrar que los fluidos obedecen de ciertas maneras sencillas¡±, a?ade.

La hip¨®tesis de Tao es que las ecuaciones de Navier-Stokes no presentar¨¢n una regularidad global, sino que ¡°explotar¨¢n¡±. Esto no significa que aparezca un tsunami de repente en el oc¨¦ano del mundo real, sino que en determinadas condiciones estas ecuaciones no sirven para describir la complejidad de los fluidos. Miranda compara la trayectoria de una part¨ªcula de un fluido con el trazo de un l¨¢piz en un papel. ¡°Explotar ser¨ªa que alguien te d¨¦ un codazo y muevas el l¨¢piz. En el dibujo ver¨ªas una discontinuidad, un comportamiento muy raro, como que se fuera al infinito¡±, ilustra la investigadora.

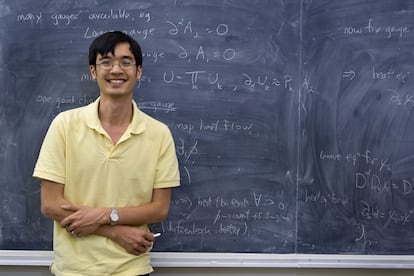
Miranda cree que si las ecuaciones de Navier-Stokes explotan ser¨ªa ¡°una aut¨¦ntica revoluci¨®n¡±, porque sugerir¨ªa que son imprecisos los modelos matem¨¢ticos para predecir el tiempo atmosf¨¦rico, la subida del nivel del mar o el comportamiento de otros fluidos viscosos esenciales, como la sangre humana y el petr¨®leo.

La m¨¢quina de agua abstracta de Miranda y sus colegas no emplea las ecuaciones de Navier-Stokes, sino una versi¨®n anterior, formulada en 1755 por el matem¨¢tico suizo Leonhard Euler para describir el movimiento de fluidos ideales, sin viscosidad. Las soluciones que ofrece la m¨¢quina no muestran saltos bruscos. ¡°Nuestra investigaci¨®n no sirve para demostrar la explosi¨®n de las ecuaciones de Navier-Stokes¡±, se?ala la catedr¨¢tica.

Eva Miranda, Daniel Peralta y Francisco Presas son miembros del Instituto de Ciencias Matem¨¢ticas (ICMAT), un centro de investigaci¨®n de excelencia en Madrid. Presas, de 46 a?os, fue entrevistado por este peri¨®dico cuando ten¨ªa 21, tras ganar un Seat Ibiza en el concurso titulado El universitario del a?o, patrocinado por la empresa automovil¨ªstica. ¡°Las matem¨¢ticas s¨ª se me dan bien¡±, declar¨® entonces. Hoy es una figura internacional en geometr¨ªa, como Miranda y Peralta. Robert Cardona hace su tesis doctoral en la Universidad Polit¨¦cnica de Catalu?a.

Puedes escribirnos a manuel@esmateria.com o seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter.