Cajas

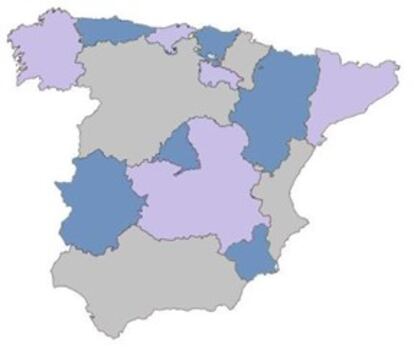
Nos pregunt¨¢bamos la semana pasada si para colorear el mapa de Andaluc¨ªa de modo que sus provincias queden claramente diferenciadas ¡ªes decir, sin que dos provincias lim¨ªtrofes sean del mismo color¡ª son necesarios cuatro colores o se puede lograr con menos. Y nos hac¨ªamos la misma pregunta con respecto a la Espa?a peninsular dividida en comunidades. Pues bien, con tres colores es suficiente tanto en el caso de las ocho provincias andaluzas como en el de las 15 comunidades peninsulares, como se ve en la figura.

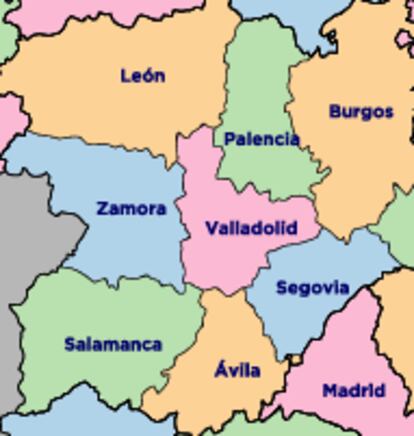
Sin embargo, para colorear de esta manera el mapa de las provincias peninsulares son necesarios cuatro colores. Para deducirlo no es necesario examinar todo el mapa: basta con darse cuenta de que hay provincias que est¨¢n rodeadas por un n¨²mero impar de vecinas. Si el n¨²mero fuera par, bastar¨ªa con dos colores alternados para colorear las provincias circundantes m¨¢s uno para la circundada, tres en total; pero si el n¨²mero es impar, la alternancia termina con dos provincias circundantes del mismo color juntas; por lo tanto, hacen falta tres colores para estas y otro para la central, que limita con todas ellas. En la figura vemos el caso de Valladolid, rodeada por otras siete provincias.

En cuanto a los sobres, el abierto puede dibujarse de un solo trazo, pero el cerrado no, porque en todos sus v¨¦rtices concurren tres aristas. Como el l¨¢piz parte de un v¨¦rtice, a los otros tres tiene que llegar, salir y volver a llegar (y ya no podr¨ªa volver a salir sin pasar otra vez por un camino ya recorrido), con lo que tendr¨ªa que terminar su itinerario en tres puntos a la vez, lo cual es obviamente imposible. En el caso del sobre abierto, sin embargo, solo hay dos v¨¦rtices (los inferiores) en los que concurren tres aristas, por lo que el recorrido del l¨¢piz puede empezar en uno de ellos y terminar en el otro. Generalizando, cuando en un nodo concurre un n¨²mero par de aristas, si el recorrido parte de ¨¦l ha de terminar en ¨¦l; y viceversa: cuando el n¨²mero de aristas concurrentes en un nodo es impar, si el recorrido parte de ¨¦l no puede terminar en ¨¦l. Como en el caso de los mapas, la paridad es la clave, puesto que, pese a que parecen problemas muy distintos, ambos se pueden esquematizar mediante grafos similares.

Del sobre a la caja

Y de los sobres rectangulares, los contenedores planos por excelencia, podemos saltar a las cajas orto¨¦dricas, los contenedores tridimensionales m¨¢s comunes. Entre ellos, el familiar tetrabrik de un litro, cuyas dimensiones son aproximadamente 20x10x5 cm (m¨¢s bien 19x9x5.9, pero el nuestro es el tetrabrik ideal plat¨®nico). Una forma elegante (cada lado es la mitad del anterior) y manejable; pero ?es ¨®ptima desde el punto de vista del aprovechamiento del material? ?Qu¨¦ ahorro ser¨ªa posible, en cent¨ªmetros cuadrados de envoltura, si optimiz¨¢ramos la relaci¨®n volumen/superficie?

Tanto las bases (10x5) como las caras laterales mayores (20x10) de nuestro tetrabrik son domin¨®s, y las caras laterales menores (20x5) son tetromin¨®s rectos (rect¨¢ngulos cuyo lado mayor es el cu¨¢druplo del menor). Teniendo esto en cuenta, ?de cu¨¢ntas maneras diferentes podemos recubrir con tetrabriks -apoy¨¢ndolos sobre cualquiera de sus caras- un tablero de ajedrez est¨¢ndar de casillas de 5 cm de lado? ?Y un tablero de damas de 10x10 casillas? ?Es posible, en uno u otro caso, alg¨²n recubrimiento sin l¨ªneas de fractura? (Ver el art¨ªculo ¡°Sin l¨ªneas de fractura¡±, del 10 12 21).

Y, para terminar, un problema propuesto por nuestro asiduo comentarista Luca Tanganelli:

Hallar todos los ortoedros de lados enteros tales que volumen + per¨ªmetro = ¨¢rea.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal