El teorema de Pappus

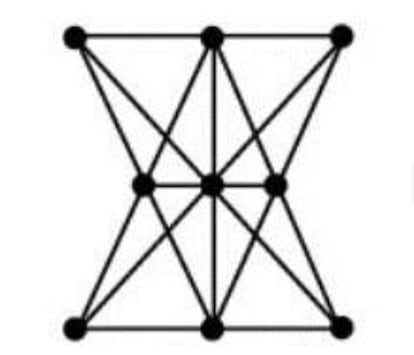
Empecemos por el ¨²ltimo problema de la semana pasada, atribuido al mism¨ªsimo Isaac Newton: ?Se pueden plantar 9 ¨¢rboles de manera que formen 10 filas rectas de 3 ¨¢rboles por fila? Se puede, como se ve en la elegante soluci¨®n de la figura adjunta. Soluci¨®n que, casualmente (es un decir: en matem¨¢ticas no existen las casualidades), ilustra el teorema de Pappus, que demuestra que si en un par de rectas se escogen tres puntos al azar en cada una y se unen dos a dos mediante segmentos rectil¨ªneos, cada punto de una recta con cada uno de los puntos de la otra, las intersecciones de los segmentos que los unen estar¨¢n en l¨ªnea recta.

Como muestra la figura, hemos tomado 3 puntos en la recta superior y 3 en la inferior, y al unir dos a dos los de ambas rectas obtenemos los 3 puntos centrales, que tambi¨¦n est¨¢n alineados. Por cierto, las rectas no tienen por qu¨¦ ser paralelas ni los puntos estar espaciados regularmente, como en este caso, para que los puntos de intersecci¨®n est¨¦n alineados.

Pappus (o Papo) de Alejandr¨ªa (c. 290-c. 350) fue el m¨¢s grande matem¨¢tico de su tiempo, y adem¨¢s de por su famoso teorema es conocido por sus trabajos sobre los s¨®lidos plat¨®nicos inscritos en una esfera y por constructos geom¨¦tricos como la cadena de Pappus, un anillo de c¨ªrculos de tama?o decreciente entre dos c¨ªrculos tangentes.

En cuanto al problema de la cuadr¨ªcula de palillos de Sam Loyd, Rafael Granero, que hall¨® una soluci¨®n retirando 10 palillos, la ha mejorado, como se ve en la figura que ha enviado, retirando solo 9.

No se pueden destruir todos los cuadrados quitando menos de 9 palillos, y me atrever¨ªa a decir (pero no estoy seguro) que, prescindiendo de giros y simetr¨ªas, la soluci¨®n es b¨¢sicamente ¨²nica. Invito a mis sagaces lectoras/es a hallar una soluci¨®n distinta o a demostrar que es ¨²nica. Lo que no es dif¨ªcil demostrar, mediante un abordaje ingenioso, es que no se pueden eliminar todos los cuadrados quitando menos de 9 palillos.

Este aparentemente sencillo pasatiempo de Sam Loyd, como a menudo ocurre con los rompecabezas geom¨¦tricos, tiene m¨¢s miga de lo que parece a primera vista y nos invita a explorar variantes de creciente complejidad. En este sentido, es interesante empezar por el principio e ir avanzando paso a paso.

En el caso trivial de un solo cuadrado de 1x1 formado por 4 palillos, es evidente que solo hay que retirar 1 para destruirlo. En el caso de 2x2, es f¨¢cil ver que hay que eliminar 3 palillos, y en el de 3x3 hay que retirar 6. No es tan f¨¢cil ver que en el de 4x4 hay que retirar un m¨ªnimo de 9 palillos. ?Y en los cuadrados de 5x5, 6x6, 7x7¡­?

?Y si no nos conformamos con destruir los cuadrados, sino que tambi¨¦n queremos eliminar todos los rect¨¢ngulos? En ese caso, tendremos que retirar 3 palillos del cuadrado de 2x2, 7 del de 3x3, 11 del de 4x4¡­ ?Te atreves a continuar?

Recolocar en vez de quitar

Por ¨²ltimo, no se puede dejar de mencionar, al hablar de los problemas con palillos o cerillas, que se dividen en dos grandes grupos: los que se resuelven retirando elementos, como los que acabamos de ver, y los que se resuelven cambiando de lugar algunos elementos, pero sin eliminar ninguno y utiliz¨¢ndolos siempre en toda su longitud. Recordemos, a modo de ejemplo, uno de los m¨¢s populares, sencillos y elegantes:

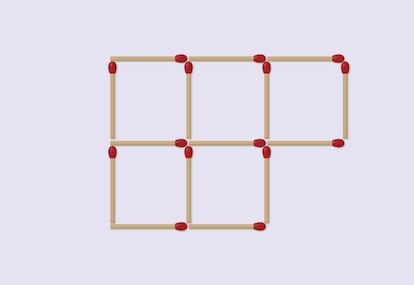
Cambiando de lugar dos cerillas, pasar de cinco cuadrados a cuatro sin que quede ninguna cerilla suelta.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.