La torre, el cubo y el tablero

La torre de Han¨®i es un popular rompecabezas ideado por el matem¨¢tico franc¨¦s ?douard Lucas a finales del siglo XIX. Consta de tres ejes verticales, en uno de los cuales se apilan un cierto n¨²mero de discos perforados de tama?os decrecientes, de mayor a menor empezando por abajo. El reto consiste en pasar todos los discos desde el eje en el que est¨¢n a uno de los otros dos, siguiendo estas sencillas reglas:

• Solo se puede mover un disco cada vez y para moverlo todos los dem¨¢s tienen que estar ensartados en alg¨²n eje.
• Un disco no puede estar sobre otro m¨¢s peque?o.
• Solo se puede mover un disco que est¨¦ en la parte superior de un eje.

Obviamente, cuantos m¨¢s discos hay, m¨¢s complicado es el traslado (en las versiones comercializadas del rompecabezas suele haber de cinco a ocho). Dada una torre de Han¨®i trivial, de un solo disco, es evidente que basta un movimiento para trasladar ese disco a otro eje. Una torre de dos discos tambi¨¦n es trivial: trasladamos el menor a uno de los dos ejes libres, el mayor al otro eje libre, y por ¨²ltimo ponemos el menor sobre el mayor. Consideremos ahora una torre de tres discos, a los que llamaremos, de menor a mayor, A, B y C. Para el primer movimiento solo hay una opci¨®n: trasladar el disco A a uno de los dos ejes libres. Para el segundo movimiento solo hay una opci¨®n no repetitiva: pasar el disco B al eje libre. Los siguientes movimientos no son ¨²nicos, pero s¨ª bastante obvios: 3) A sobre B, 4) C al eje libre, 5) A al eje libre, 6) B sobre C, 7) A sobre B. La secuencia es, pues, ABACABA.

El cubo

Como vimos la semana pasada, Hamilton estudi¨® en los s¨®lidos plat¨®nicos los recorridos que llevan su nombre, que consisten en pasar una y solo una vez por todos los v¨¦rtices. En el caso de un cubo, si llamamos A a la direcci¨®n vertical, B a la horizontal y C a la anteroposterior, partiendo, por ejemplo, del v¨¦rtice superior izquierdo del cubo y yendo primero hacia abajo, luego hacia la derecha, luego hacia arriba, luego hacia atr¨¢s y as¨ª hasta completar el sencillo recorrido hamiltoniano, veremos que la secuencia direccional (y dimensional) es ABACABA, la misma que en una torre de Han¨®i de tres discos. ?Mera casualidad? Invito a mis sagaces lectoras/es a comprobarlo, hallando la secuencia de traslados para una torre de cuatro discos, y luego buscando un camino hamiltoniano que recorra los v¨¦rtices de un hipercubo (para quien no tenga acceso directo a la cuarta dimensi¨®n, puede servir una proyecci¨®n tridimensional como la de la figura adjunta). ?Se observa alguna semejanza entre ambos recorridos?

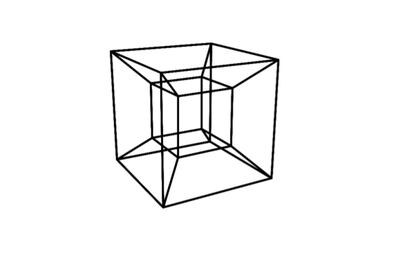
El tablero

Seg¨²n una conocida leyenda, el m¨ªtico inventor del ajedrez le pidi¨® al rey de la India un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta, y as¨ª sucesivamente hasta la casilla 64, doblando en cada una el n¨²mero de granos de trigo de la anterior. Pues bien, este n¨²mero (18.446.744.073.709.551.615) es igual al n¨²mero de traslados necesarios para pasar de un eje a otro todos los discos de una torre de Han¨®i de 64 discos, tantos como casillas tiene el tablero de ajedrez. ?Otra coincidencia?

Por cierto, si los 64 discos son de oro y los ejes son agujas de diamante, nos hallamos ante la leyenda (ap¨®crifa) de la torre de Brahma, seg¨²n la cual el mundo se acabar¨¢ cuando los sacerdotes del templo de Benar¨¦s terminen de trasladar todos los discos a otro eje. Pero que no cunda el p¨¢nico: aunque los diligentes monjes trasladaran un disco por segundo sin descansar ni un momento, el apocalipsis no ser¨ªa inminente.

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.