Redes matem¨¢ticas para entender conflictos sociales

En la famosa serie televisiva Juego de tronos, las diferentes casas nobiliarias en el continente llamado Poniente luchan por gobernar los siete reinos que conforman el territorio. Para ello, establecen relaciones de alianza y enemistad con las otras casas. Si tres casas forman una triple alianza constituyen un sistema estable, ya que no hay tensiones entre sus componentes. Sin embargo, ?qu¨¦ pasa con la estabilidad de los sistemas en los que dos casas aliadas no coinciden en la consideraci¨®n de una tercera, para una es amiga y para otra enemiga?

Para estudiar este tipo de sistemas, Frank Harary formaliz¨® el concepto matem¨¢tico de balance en 1954, basado en la teor¨ªa del balance social del psic¨®logo Fritz Heider. Harary propon¨ªa describir las relaciones en una red cuyos nodos (puntos) representan las entidades del sistema, y las aristas (uniones entre puntos), que llevan signos positivos o negativos, representan las relaciones entre dichas entidades. Las relaciones de alianza se identifican con un signo positivo (+) y aquellas de enemistad con un signo negativo (-). En este contexto un ciclo (es decir, una sucesi¨®n de relaciones que empiezan y acaban en el mismo elemento) es balanceado si el producto de sus signos es positivo. Y si todos los ciclos de una red son balanceados, entonces la red lo es.

El resultado fundamental de su trabajo fue el teorema estructural del balance, que ofrece una manera de identificar las redes balanceadas sin tener que comprobar uno a uno todos sus ciclos. Seg¨²n este teorema, una red con signos es balanceada siempre y cuando es posible partir su conjunto de v¨¦rtices en dos partes, de tal forma que cada arista positiva conecta v¨¦rtices del mismo subconjunto y las aristas negativas conectan v¨¦rtices entre los dos subconjuntos.

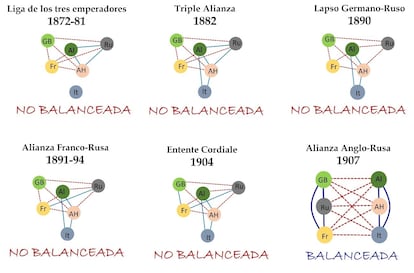
Por ejemplo, consideremos las alianzas y conflictos entre las principales potencias europeas a finales del siglo XIX y principios del XX, representadas en la imagen inferior. Las relaciones de alianza se han representado en color azul y las de enemistad en rojo. Aplicando el teorema anterior puede determinarse que solo con la alianza Anglo-Rusa de 1907 en la que Gran Breta?a, Rusia y Francia formaron una triple-alianza y Alemania, el imperio Austro-H¨²ngaro e Italia formaron otra, ambas enfrentadas entre s¨ª, se logr¨® que este sistema fuera balanceado. Este balance permanec¨ªa en 1914 cuando estall¨® la Primera Guerra Mundial (Figura 1).

M¨¢s all¨¢ de decidir si una red es o no balanceada, tambi¨¦n es posible cuantificar su grado de balance, como estudi¨® el propio Harary. Se han propuesto diversas medidas, pero la mayor¨ªa requieren de aproximaciones computacionales o no tienen en cuenta todos los ciclos de la red. En 2014, el autor de este art¨ªculo y el matem¨¢tico Michele Benzi propusieron una caracterizaci¨®n cuantitativa del grado de balance de una red. Esta medida est¨¢ basada en el c¨¢lculo del espectro de la red.

Para hacerlo, la red se representa en forma de una tabla cuyas entradas pueden ser +1, si los pares de nodos correspondientes tienen una relaci¨®n positiva; -1, si la tienen negativa y cero, si no tienen relaci¨®n. Usando m¨¦todos del ¨¢lgebra lineal se descompone esta tabla en lo que se llama su espectro de valores propios. Aplicando un teorema matem¨¢tico, sabemos que si partimos de una red inicial balaceada, su espectro es id¨¦ntico al de la red que se obtiene al transformar la red, cambiando cada valor negativo por uno positivo. El ¨ªndice de balance cuantifica precisamente cuan alejado est¨¢ el espectro de una red al de la red en la que todas las relaciones son positivas. Por tanto, su valor es uno si la red es balanceada y se aproximar¨¢ a cero en la medida que la red sea cada vez menos balanceada.

Esta caracterizaci¨®n ha permitido descubrir que muchas redes del mundo real est¨¢n muy lejos del balance, en contra de la hip¨®tesis de Fritz Heider, que propon¨ªa que los sistemas sociales tender¨ªan al balance. Por ejemplo, la red de alianzas y conflictos entre las tribus que habitan la regi¨®n de Gahuku-Gama en Pap¨²a Nueva Guinea tiene un grado de balance de aproximadamente 1/3. Otras redes, como la que forman las votaciones para elegir a los administradores de Wikipedia, en las que las conexiones son positivas si ambos votantes votan a favor del mismo candidato, y negativas si lo hacen en contra, tiene un balance de 0.00001.

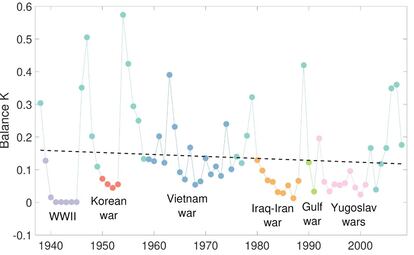
Tambi¨¦n se aplicaron estas ideas para analizar las redes de alianzas y conflictos entre las diferentes naciones del mundo entre los a?os 1938 y 2008, con que datos fueron aportados por el investigador Zeev Maoz. Los resultados indican (ver Fig. 2) que el mundo no se dirige a un estado de balance. Adem¨¢s, se observa que los per¨ªodos de alto grado de balance fueron casi siempre seguidos por conflictos armados de gran envergadura. Es como si los balances de fuerza dieran la confianza a las partes a ensalzarse en la lucha contra los otros. Y por tanto, quiz¨¢ debamos evitarlos. Quiz¨¢ el bajo grado de balance existente en el a?o 1962 oblig¨® a las partes a encontrar una soluci¨®n a la crisis de los misiles de Cuba.

Ernesto Estrada es profesor de investigaci¨®n del Consejo Superior de Investigaciones Cient¨ªficas en el Instituto de F¨ªsica Interdisciplinar y Sistemas Complejos, en la Universidad de las Islas Baleares en Palma de Mallorca.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.