Nudos que representan n¨²meros, las matem¨¢ticas de los incas

Uno de los mantras favoritos de los matem¨¢ticos se atribuye a Galileo Galilei: el universo est¨¢ escrito en clave matem¨¢tica. Sin embargo, aunque las matem¨¢ticas son un lenguaje universal, la manera en que las describimos puede ser muy diferente. Por ejemplo, frente a la necesidad b¨¢sica de contar, se desarroll¨® el concepto de n¨²mero. Pero, en cada lugar, las matem¨¢ticas se vistieron con ropajes muy diversos para capturar la informaci¨®n de las cantidades: los babilonios usaban el sistema sexadecimal y escrib¨ªan los n¨²meros con muescas en tablillas de arcillas; los griegos usaban letras; los incas, los llamados quipus, que eran cuerdas anudadas. Los quipus han vuelto a la actualidad con la reciente publicaci¨®n de la monumental novela El esp¨ªa del Inca (Alfaguara), del peruano Rafael Dumett, protagonizada por un tejedor de quipus, dotado de extraordinarias habilidades aritm¨¦ticas.

Los quipus fueron inventados para poder enviar informaci¨®n, a veces codificada, desde cualquier punto del imperio ¡ªque se extend¨ªa por gran parte de Sudam¨¦rica y era tan extenso y variado como el imperio romano¡ª a la capital, Cuzco. La palabra quipu proviene del quechua y significa nudo. As¨ª, los quipus son nudos que sirven para representar conceptos matem¨¢ticos ¡ªn¨²meros¡ª; siglos m¨¢s tarde, las matem¨¢ticas modernas se ocupar¨¢n a su vez de estudiar y clasificar los nudos (con los extremos unidos).

El quipu m¨¢s antiguo data del a?o 2.500 a.C. y fueron utilizados hasta la colonizaci¨®n del imperio espa?ol. Los conquistadores espa?oles los consideraron objetos id¨®latras y peligrosos, por lo que destruyeron muchos de ellos inciner¨¢ndolos. Los quipus normalmente estaban hechos de algod¨®n o lana de pelo de llama o alpaca. Se construyen con una cuerda principal, sin nudos, de la cual penden otras anudadas y de diversos colores, formas y tama?os. Los colores identifican sectores ¡ªpor ejemplo, pardo es el correspondiente al gobierno; carmes¨ª, es el del propio Inca, soberano del imperio; rojo, la guerra¡ª mientras que los nudos indican cantidades ¡ª incluyendo el n¨²mero cero, la ausencia de nudos¡ª.

Cada cuerda contiene un grupo de nudos que representan un n¨²mero. En el libro C¨®digo del quipu: un estudio en medios, matem¨¢ticas y cultura, Marcia Ascher y Robert Ascher determinan, tras analizar cientos de quipus, que existen tres tipos fundamentales de nudos: simples, que son nudos de una vuelta ¡ªy que, en el libro, se representan con una s¡ª; largos, consistentes en un nudo con una o m¨¢s vueltas adicionales (L); y con forma de ocho (E).

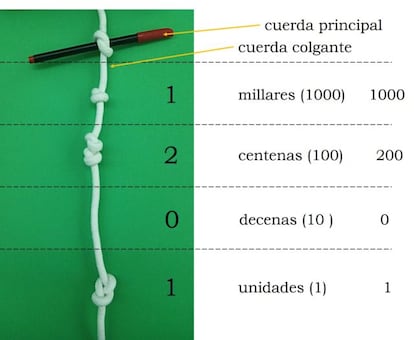
Los quipus emplean, como nuestros n¨²meros indo-ar¨¢bigos, la base decimal. Es decir, en la cuerda se diferencian posiciones, en cada una de las cuales se indican el n¨²mero de unidades, decenas, centenas, millares, etc. que tiene el n¨²mero representado. Los d¨ªgitos en la posici¨®n de unidades son representados por nudos largos¡ªpor ejemplo, el 4 es un nudo con cuatro vueltas¡ª. Debido a la forma en que los nudos se atan, el 1 no puede ser mostrado de esta manera y est¨¢ representado en esa posici¨®n por una figura en forma de ocho.

En las posiciones superiores ¡ªdecenas, centenas, etc.¡ª las cifras est¨¢n representadas por grupos de nudos simples ¡ªpor ejemplo, 40 se escribe con cuatro nudos simples seguidos, en la posici¨®n decena¡ª. El cero es representado por la ausencia de un nudo en la posici¨®n apropiada. En el sistema de los Ascher, lo denotan con una X. As¨ª, 804 quedar¨ªa descrito por 8s, X, 4L.

Los responsables de elaborar los quipus eran los llamados quipucamayoc, que aprend¨ªan su oficio en la yachay wasi o casa de ense?anza. Los quipucamayoc sab¨ªan sumar, restar, multiplicar y dividir, pero no se trataba de meros contables, ya que pertenec¨ªan a la nobleza, deb¨ªan tener m¨¢s de cincuenta a?os y formaban una casta cerrada.

Los quipucamayoc no empleaban los quipus para realizar operaciones ¡ªestos serv¨ªan ¨²nicamente para almacenar y transmitir informaci¨®n¡ª sino una especie de ¨¢baco, llamado yupana, o el quipu de granos de ma¨ªz. No se sabe muy bien c¨®mo funcionaba, pero se cree que era parecido a otros ¨¢bacos desarrollados en Europa y Oriente. En la novela de Dumett se describe como aprende por s¨ª mismo a usarlo observando a los comerciantes.

Esta informaci¨®n, como mucha otra de la cultura inca, desapareci¨® tras la llegada de los espa?oles; los incas no desarrollaron escritura, por lo que no quedaron registros escritos. Parte de sus matem¨¢ticas s¨ª qued¨® capturada en nudos de cuerda que uno no puede dejar de preguntarse como hubieran evolucionado sin la conquista espa?ola.

Manuel de Le¨®n es profesor de investigaci¨®n del Consejo Superior de Investigaciones Cient¨ªficas en el ICMAT y miembro de la Real Academia de Ciencias Exactas, F¨ªsicas y Naturales

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.