La eterna batalla de crear y destruir c¨®digos: 80 a?os de la m¨¢quina Enigma

En 2023 se cumplen 80 a?os de un evento clave durante el transcurso de la Segunda Guerra Mundial: el desencriptado de la m¨¢quina Enigma por parte del bando aliado (gracias a la distinguida labor del matem¨¢tico Alan Turing, entre otros). Este dispositivo era utilizado por los alemanes para transmitir planes militares de forma secreta, por lo que su descifrado influy¨® notablemente en el transcurso de la guerra, a la vez que supuso un notable avance dentro de la criptograf¨ªa. El rumbo de la disciplina est¨¢ muy determinado por un conflicto perpetuo: mientras que unos buscan transmitir informaci¨®n de forma segura mediante cifrados, otros intentar¨¢n romper esos c¨®digos para acceder a la informaci¨®n. Esto produce cada vez mejores sistemas.

Los primeros cifrados en aparecer fueron los de sustituci¨®n monoalfab¨¦ticos. Su funcionamiento es muy sencillo: cada letra del mensaje original se cambia por otro car¨¢cter para producir un mensaje cifrado. Por ejemplo, todas las ¡°e¡± se cambian por ¡°g¡±. El problema de este sistema es que la frecuencia de las letras del texto original se transmite al texto cifrado. As¨ª, si en el mensaje cifrado hay muchas ¡°g¡± y ¡°q¡±, estas probablemente se correspondan con la ¡°e¡± y ¡°a¡±, las letras m¨¢s frecuentes en un texto en espa?ol. Con esta idea, desarrollada en la t¨¦cnica de an¨¢lisis de frecuencias, podr¨ªamos empezar a romper el c¨®digo. El relato El escarabajo de oro, de Edgar Allan Poe, entrelaza la historia con una explicaci¨®n detallada de este m¨¦todo.

En respuesta a esta debilidad, aparecieron los cifrados de sustituci¨®n polialfab¨¦ticos. En ellos, una letra no siempre se cifra al mismo car¨¢cter, ya que la regla de sustituci¨®n va cambiando a lo largo del texto. En los ejemplos cl¨¢sicos de estos sistemas, como el cifrado Vigen¨¨re, se usan pocas reglas de sustituci¨®n y es f¨¢cil agrupar las letras del texto cifrado seg¨²n con qu¨¦ norma se ha obtenido cada una. Una vez separadas las letras por grupos, cada uno de ellos es un texto encriptado mediante un cifrado por sustituci¨®n monoalfab¨¦tico, as¨ª que se puede aplicar an¨¢lisis de frecuencias.

Aunque la m¨¢quina Enigma lleva a cabo este mismo tipo de cifrado polialfab¨¦tico, supuso un gran avance respecto a las t¨¦cnicas cl¨¢sicas. Cuenta con tres rotores que establecen una conexi¨®n entre un teclado y un panel luminoso. Al pulsar una tecla, se ilumina la letra a la que se cifra y la configuraci¨®n de los rotores cambia, de forma que para la letra siguiente se utiliza una regla distinta. Los detalles del mecanismo interno hacen que se usen una cantidad enorme de reglas distintas, lo que hace extremadamente dif¨ªcil romper el c¨®digo: solo es posible si se conoce la configuraci¨®n inicial de la m¨¢quina. Peque?os problemas del sistema, junto con los avances matem¨¢ticos y computacionales de varios a?os de trabajo y alguna dosis de suerte, permitieron finalmente descifrar la Enigma.

Una de estas flaquezas era la necesidad de distribuir de antemano informaci¨®n sobre la configuraci¨®n de las m¨¢quinas, corriendo el riesgo de que pudiera ser interceptada. La dificultad de intercambiar claves de forma segura era, por tanto, el siguiente problema a solucionar para hacer sistemas m¨¢s robustos. La respuesta no lleg¨® hasta los a?os 70 del siglo pasado, con el protocolo Diffie¨CHellman.

Supongamos que Antonio y Beatriz quieren cifrar sus comunicaciones, para lo que necesitar¨¢n acordar una clave secreta. Este protocolo elimina la necesidad de quedar en persona para hacerlo. Se suele explicar el proceso matem¨¢tico subyacente como si fuera una mezcla de diferentes pinturas. Ambos agentes deciden un color de uso com¨²n, que no es necesario que se mantenga en secreto. Y cada uno elige tambi¨¦n un color de forma secreta, que solo conocen ellos mismos. Al mezclar sus colores con la pintura com¨²n, obtienen dos nuevos colores diferentes, que ser¨¢n la informaci¨®n que env¨ªen.

Si alguien intercepta la informaci¨®n, tendr¨¢ dificultad para conocer sus colores secretos: aunque conozcan el color ¡°p¨²blico¡±, separar la mezcla para determinar los colores que la forman es un proceso muy costoso. Sin embargo, ellos, cuando la reciben, pueden volver a a?adir su color secreto, obteniendo as¨ª una mezcla de los mismos tres colores, que ser¨¢ su secreto en com¨²n. Para que un interceptor consiga la misma mezcla final, tendr¨ªa que separar una de las mezclas enviadas y a?adir el color privado resultante a la otra. Como esto es inviable, al ser demasiado costoso, el protocolo es seguro.

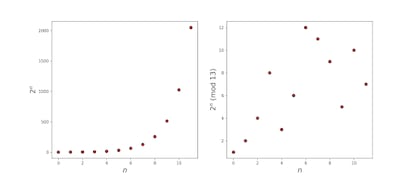
En la realidad, este proceso no se hace con pintura, sino con matem¨¢ticas. Su seguridad se basa en una operaci¨®n r¨¢pida de calcular en un ordenador, la exponenciaci¨®n en aritm¨¦tica modular, pero que es muy dif¨ªcil deshacer sabiendo solo el resultado. Mientras que la exponenciaci¨®n usual sigue un patr¨®n claro, la exponenciaci¨®n en aritm¨¦tica modular es muy dif¨ªcil de predecir y, por tanto, de deshacer. Esto se conoce como el problema del logaritmo discreto.

Pero antes de acordar una clave com¨²n, los involucrados en la comunicaci¨®n tienen que poder comprobar que la otra persona no es un impostor. Para ello, se utilizan certificados de autentificaci¨®n. Una vez hecho esto, ya se puede usar el m¨¦todo de Diffie¨CHellman para acordar una clave secreta, y finalmente enviar informaci¨®n cifrada. Los procesos reales son mucho m¨¢s elaborados que lo descrito aqu¨ª, pero estos son ingredientes fundamentales, y son esenciales para la comunicaci¨®n de forma segura en internet. Aunque el campo sigue en constante evoluci¨®n, estos protocolos llevan muchos a?os siendo completamente seguros. Sin embargo, nunca faltar¨¢ gente que intente romperlos, por lo que la batalla criptogr¨¢fica nunca finaliza.

Laura Castilla Castellano y Javier Pe?afiel Tom¨¢s son investigadores predoctorales en la Universidad Complutense de Madrid y el Consejo Superior de Investigaciones Cient¨ªficas, respectivamente, y miembros del Instituto de Ciencias Matem¨¢ticas

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.