Eugenio Calabi, el matem¨¢tico cautivado por la belleza del espacio

El matem¨¢tico italiano Eugenio Calabi falleci¨® el pasado 25 de septiembre de 2023 a la edad de 100 a?os en Beaumont, Bryn Mawr (EE UU). Este a?o se hab¨ªan sucedido numerosos homenajes a lo largo y ancho del mundo, para celebrar su imponente legado e importantes contribuciones a la geometr¨ªa. Es inusual que el centenario de un importante matem¨¢tico, con m¨¢s de 70 a?os de herencia cient¨ªfica, y tres generaciones de descendientes, se celebre ante la mirada atenta del mismo ¨Cas¨ª sucedi¨® en uno de los congresos, celebrado en Hefei (China)¨C.

Nacido en Mil¨¢n (Italia) en mayo de 1923, Calabi se mud¨® a los Estados Unidos junto con su familia a una edad temprana. Curso sus estudios en el Massachusetts Institute of Technology, financiado con una prestigiosa beca Putnam, que tambi¨¦n recibieron otros como Richard P. Feynman, Premio Nobel de F¨ªsica, y John Milnor, Medalla Fields. En 1950 ley¨® su tesis en la Universidad de Princeton sobre propiedades de ciertos espacios geom¨¦tricos conocidos como variedades de K?hler. Tras trabajar como profesor en la Universidad de Minnesota, en 1964 Calabi se incorpor¨® a la Universidad de Pensilvania. Pocos a?os m¨¢s tarde, obtuvo la prestigiosa c¨¢tedra Thomas A. Scott Professor of Mathematics, que ocup¨® hasta su jubilaci¨®n en 1994, cuando se convirti¨® en profesor em¨¦rito en la misma instituci¨®n.

Su trabajo ha dejado una profunda huella en la geometr¨ªa moderna. Su obsesi¨®n era dotar al espacio desnudo de una forma ¡°preferida¡±, como el que moldea una pieza de arcilla con sus manos en busca de una figura oculta, nunca antes imaginada. Por ejemplo, al posar una cuerda atada por sus extremos sobre una superficie plana, ?cu¨¢l es la forma preferida que puede adoptar? La respuesta de muchos ser¨¢ una circunferencia, porque es ¡°igual por todas partes¡± o, tal vez, porque es ¡°la figura m¨¢s perfecta¡±. Un matem¨¢tico podr¨ªa a?adir que esta percepci¨®n tiene que ver con una propiedad variacional de dicha curva: es la que maximiza el ¨¢rea total que encierra en su interior.

Un m¨¦todo matem¨¢tico para encontrar estas curvas preferidas en el plano ¨Cdenominado flujo de curvatura media¨C es el siguiente: se parte de una curva cualesquiera (que no se corte a s¨ª misma) y se la hace ¡°evolucionar¡± de manera que pierde ¨¢rea a velocidad constante y su per¨ªmetro decrece lo m¨¢s r¨¢pidamente posible. Con el tiempo la curva ser¨¢ convexa, y tender¨¢ a un c¨ªrculo de radio cada vez m¨¢s peque?o hasta colapsar en un punto. Momentos antes de este colapso, se observa a simple vista la forma preferida de la curva a una escala muy peque?a.

Si la curva inicial se cortase a s¨ª misma, puede desarrollar una singularidad o ¡°pico¡± a lo largo de su evoluci¨®n y esto cambia la forma preferida de la curva. Al situarse en el lugar de la singularidad justo antes de que se forme, se observa, mediante un cambio de escala, la evoluci¨®n ¡°autosimilar¡± de una curva que proviene de un pasado infinito: una curva que no var¨ªa su forma mientras evoluciona con el tiempo. En este caso, adem¨¢s, la curva se mueve por traslaciones, es decir, todos sus puntos se desplazan a velocidad constante en una direcci¨®n fija. Eugenio Calabi descubri¨® esta soluci¨®n al flujo de curvatura media en los a?os 1980 y la bautizo como La Parca (the Grim Reaper).

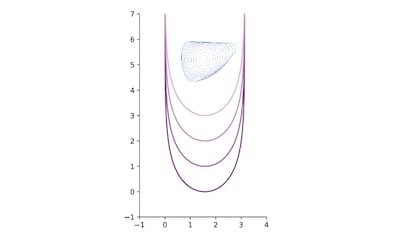
Parece que Calabi hizo este descubrimiento en una pausa para tomar el t¨¦, en medio de una conversaci¨®n, rodeado de sus colegas. La Parca resulta ser la ¨²nica soluci¨®n definida desde un tiempo pasado infinito del flujo de curvatura media que evoluciona por traslaciones: una propiedad esencial que tan solo ser¨ªa entendida muchos a?os m¨¢s tarde. Esta es posiblemente una de las caracter¨ªsticas m¨¢s singulares de Calabi: su influencia en el trabajo de sus colegas se produc¨ªa muchas veces a trav¨¦s de largas conversaciones informales o c, con observaciones agudas y ejemplos clave, que m¨¢s tarde se convertir¨ªan en piezas fundamentales de futuras teor¨ªas matem¨¢ticas. En palabras de Edoardo Vesentini (investigador de la Scuola Normale Superiore di Pisa): ¡°en las teor¨ªas m¨¢s intimidatorias y en aquellos teoremas que m¨¢s me atormentaban, llegaban las sencillas explicaciones de Calabi¡±.

En su caso, estas explicaciones parec¨ªan provenir de una intuici¨®n o gusto est¨¦tico. Seg¨²n explicaba el propio Calabi en una visita a Espa?a en septiembre del a?o 2000: ¡°La fuente principal de la intuici¨®n geom¨¦trica est¨¢, en ¨²ltima instancia, ligada a nuestras percepciones sensoriales del mundo. Por supuesto, a medida que llegamos a ¨¢reas m¨¢s abstractas, uno tiene que interpretar lo que significa experiencia sensorial. Yo he tratado de hacer esto lo m¨¢s visible posible para transmitir esta idea.¡±

El placer del descubrimiento puro y la belleza de la geometr¨ªa eran, de hecho, dos motores de las matem¨¢ticas de Calabi. Sin embargo, su trabajo ha resultado tener importantes implicaciones en otros campos aplicados, como la f¨ªsica te¨®rica. Tal y como describ¨ªa el propio Calabi, los matem¨¢ticos ¡°inventan mundos imaginarios, y los cient¨ªficos deciden mucho m¨¢s tarde si estos pueden albergar genuinas teor¨ªas cient¨ªficas¡±. Uno de estos mundos imaginado por Calabi naci¨® de estudiar la forma preferida de una clase importante de espacios geom¨¦tricos conocidos como variedades complejas. Estos objetos se hacen r¨ªgidos al dotarlos con una noci¨®n de distancia (llamada m¨¦trica de K?hler). La forma preferida de este espacio viene dada por elegir, de entre todas las posibles m¨¦tricas, la que hace que el espacio se curve de forma m¨¢s homog¨¦nea. Un caso particular de este problema se conoce como el problema de Calabi. Durante m¨¢s de 20 a?os, grandes matem¨¢ticos trataron de abordarlo, llegando a soluciones contradictorias. Por fin, en 1978, Shing-Tung Yau lo resolvi¨®, dando lugar a los espacios popularmente conocidos como variedades Calabi-Yau. Por este importante logro, la comunidad matem¨¢tica internacional distingui¨® al matem¨¢tico chino con la Medalla Fields en 1982. A d¨ªa de hoy, el problema general inicialmente puesto por Calabi contin¨²a abierto y ha tenido una gran repercusi¨®n en el desarrollo de la geometr¨ªa compleja del siglo XX y principios del XXI. Gran parte de la actividad se ha centrado durante a?os en el estudio de las geometr¨ªas conocidas como K?hler-Einstein, del cual las variedades Calabi-Yau son un caso particular.

El criterio de Calabi para encontrar la forma preferida del espacio result¨®, a?os despu¨¦s, tener una profunda relaci¨®n con las ecuaciones de campo de la relatividad general introducidas por Albert Einstein. En estas ecuaciones, la distribuci¨®n de materia y energ¨ªa en el espacio determina la curvatura del mismo. En ausencia de materia, o cuando fijamos una distribuci¨®n homog¨¦nea de la misma, el espacio adopta la forma preferida imaginada por Eugenio Calabi. Sorprendentemente, lejos de ser una mera analog¨ªa, los espacios de Calabi-Yau, con sus bellas formas geom¨¦tricas, juegan un papel clave en algunas teor¨ªas f¨ªsicas modernas que abordan el problema de la gravedad cu¨¢ntica, como la conocida teor¨ªa de supercuerdas.

Mario Garc¨ªa Fern¨¢ndez es investigador Ram¨®n y Cajal en la Universidad Aut¨®noma de Madrid y miembro del Instituto de Ciencias Matem¨¢ticas (ICMAT).

?scar Garc¨ªa-Prada es profesor de investigaci¨®n del Consejo Superior de Investigaciones Cient¨ªficas y miembro del ICMAT.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.