El tetraedro y la serpiente

La f¨®rmula de Pick, que, como se dijo la semana pasada, permite hallar la superficie de un pol¨ªgono reticular en funci¨®n de sus puntos interiores y perimetrales, no puede ser m¨¢s sencilla:

S = i + p/2 -1

donde i es el n¨²mero de puntos interiores y p el n¨²mero de puntos perimetrales. Las distintas maneras de demostrar este teorema dieron lugar a una animada discusi¨®n entre los lectores, en la que se lleg¨® a plantear si el de Pick es un verdadero teorema o, simplemente, ¡°una f¨®rmula que funciona¡±, como argument¨® Francisco Montesinos (ver la primera veintena de comentarios de la entrega anterior). La cuesti¨®n no es balad¨ª, pues entre lo que llamamos ¡°teoremas¡± y lo que llamamos ¡°propiedades¡± la diferencia no es cualitativa sino de grado, ya que en cualquier premisa matem¨¢tica est¨¢n presentes todas sus implicaciones. ?Es un teorema que la suma de los ¨¢ngulos de un tri¨¢ngulo es 180?? ?Y la igualdad de los ¨¢ngulos opuestos por el v¨¦rtice? Se podr¨ªa argumentar que esto ¨²ltimo es evidente (basta con darse cuenta de que tienen el mismo ¨¢ngulo suplementario, es decir, de que les falta lo mismo para llegar a 180?); pero el concepto de ¡°evidente¡± es muy subjetivo, y nos remite, una vez m¨¢s, a la vieja paradoja sorites o ¡°del mont¨®n¡±, de la que ya nos hemos ocupado en m¨¢s de una ocasi¨®n. Manuel Amor¨®s lo ha expresado de una manera no por humor¨ªstica menos elocuente: ¡°Si no me cuesta entenderlo, es f¨®rmula; si me cuesta entenderlo, es lema: si no entiendo un pimiento, es teorema¡±. (Cabr¨ªa a?adir: si lo entiendo, pero no puedo demostrarlo, es conjetura).

En cuanto a la tentaci¨®n de ampliar el teorema de Pick al espacio tridimensional, John Reeve demostr¨® en 1957 que no es posible, a partir del siguiente contraejemplo:

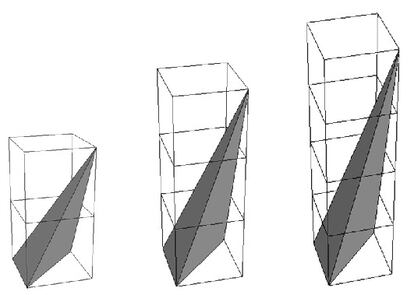
Consideremos un tetraedro cuyos v¨¦rtices son los puntos (0, 0, 0), (0, 1, 0), (1, 0, 0) y (1, 1, r) de unos ejes de coordenadas espaciales, donde r es un n¨²mero natural (entero y positivo). En la figura adjunta, vemos el tetraedro de Reeve, de base fija y altura variable, cuando r toma los valores 2, 3 y 4 respectivamente. ?De qu¨¦ manera este tetraedro demuestra la inaplicabilidad del teorema de Pick en el espacio 3D? Y tras esta pregunta de dificultad media, una f¨¢cil y otra dif¨ªcil: ?Cu¨¢l es el volumen del tetraedro de Reeve? ?Es aplicable la conclusi¨®n de inaplicabilidad del teorema de Pick en 3D a otras dimensiones?

En cuanto a las cuestiones relativas al ostomachion, al parecer no han despertado, por ahora, el inter¨¦s de mis sagaces lectoras/es (no puedo creer que se les resistan), as¨ª que quedan pendientes.

El juego de la serpiente

Volviendo desde la ret¨ªcula tridimensional a la cuadr¨ªcula bidimensional por excelencia, el tablero de 8x8, y retomando el tema de los juegos de estrategia segura abordado en semanas anteriores, Ignacio Alonso propone un problema procedente de la muy recomendable colecci¨®n de puzles matem¨¢ticos de Peter Winkler:

Ad¨¢n empieza su juego de la serpiente (nada que ver con el de Google) marcando una casilla cualquiera de un tablero de ajedrez. A continuaci¨®n, Eva marca una casilla ortogonalmente adyacente a la marcada por su compa?ero. Y as¨ª, por turnos, van marcando cada uno una casilla adyacente a la ¨²ltima marcada, formando una serpiente en el tablero. El juego termina cuando uno de los dos no puede marcar ninguna casilla, y con ello pierde la partida.

?Hay alguna casilla que garantice la victoria de Ad¨¢n si la marca en su primera jugada? Dicho de otro modo: ?es el de la serpiente de Winkler un juego de estrategia segura?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.