El eterno tri¨¢ngulo

El problema de los apretones de manos planteado la semana pasada (y directamente relacionado con uno de los ¡°problemas matrimoniales¡± de hace un par de meses) ha suscitado numerosos e interesantes comentarios, aunque en realidad es bastante simple, si se enfoca de la forma adecuada. Todos los apretones de manos son dobles, pues consisten en juntar dos manos que se aprietan mutuamente, por lo que el n¨²mero total de ¡°acciones manuales¡± (AM) ha de ser par. Evidentemente, el n¨²mero de AM de las personas que han dado la mano un n¨²mero par de veces es par, luego el n¨²mero de AM de las personas que han dado la mano un n¨²mero impar de veces tambi¨¦n ha de ser par, para que la suma total lo sea; pero si el n¨²mero de estas ¨²ltimas fuera impar, tambi¨¦n lo ser¨ªa la suma de sus AM, luego el n¨²mero de personas que han dado la mano un n¨²mero impar de veces tiene que ser par. Parece un trabalenguas, pero en realidad es bastante sencillo.

Para que un n¨²mero sea divisible por 9 al restarle la suma de sus cifras no ha de cumplir condici¨®n alguna. Dado un n¨²mero de tres cifras cualquiera, abc, si le restamos la suma de sus cifras (a + b + c) tenemos: 100a + 10b + c ¨Ca ¨C b ¨C c = 99a + 9b, que es divisible por 9 cualesquiera que sean a y b. Obviamente, el razonamiento sigue siendo v¨¢lido para n¨²meros de m¨¢s de tres cifras y, por lo tanto, cualquier n¨²mero entero es divisible por 9 si le restamos la suma de sus cifras. Por eso la condici¨®n necesaria y suficiente para que un n¨²mero sea divisible por 9, es que lo sea la suma de sus cifras.

Como ha se?alado Jordi Ferrer, el problema de la parcela no est¨¢ bien planteado, pues la intensidad del sonido en un punto dado no depende de su distancia al foco sino del cuadrado de dicha distancia. Aclarado lo cual, se da la curiosa circunstancia de que la suma de las distancias a los tres lados es la misma para cualquier punto de la parcela.

El ¨¢rea (S) del tri¨¢ngulo equil¨¢tero de la figura es la suma de los tres tri¨¢ngulos obtenidos al unir un punto cualquiera con los tres v¨¦rtices; si llamamos l al lado del tri¨¢ngulo, S = la/2 + lb/2 + lc/2 = l(a + b + c)/2, por lo que a + b + c es constante e igual a la altura del tri¨¢ngulo, h, ya que S = lh/2. Es el conocido (al menos para los estudiantes italianos) teorema de Viviani.

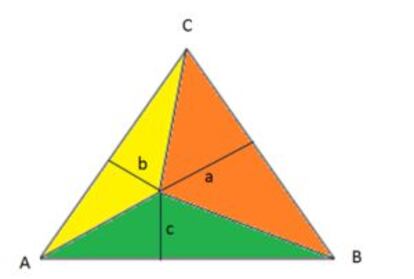
M¨¢s tri¨¢ngulos

Manuel Amor¨®s propone otro interesante problema af¨ªn al anterior: hallar, en un tri¨¢ngulo cualquiera que no tenga un ¨¢ngulo mayor o igual a 120?, un punto tal que la suma de sus distancias a los v¨¦rtices sea m¨ªnima.

En la misma l¨ªnea, demostrar gr¨¢ficamente que las tres alturas de un tri¨¢ngulo cualquiera se cortan en un punto.

Y, para terminar, pasemos de los tri¨¢ngulos geom¨¦tricos a los amorosos:

Antonio, Bernardo y Clara juegan a la pelota en la playa. Bernardo est¨¢ enamorado de Clara, y cada vez que tiene la pelota se la tira a ella (que es una forma de tirar los tejos). Clara est¨¢ enamorada de Antonio, y cada vez que tiene la pelota se la tira a ¨¦l. Antonio no se da por aludido, y tira la pelota indistintamente a Bernardo o a Clara. ?Cu¨¢l es la probabilidad de que cada uno de los tres tenga la pelota en un momento dado?

Carlo Frabetti

Escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York, ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯