El infinito y m¨¢s ac¨¢
?Es infinito el n¨²mero de libros escribibles? ?Y el n¨²mero de cuadros pintables?

Llamando d a la diagonal de un cuadrado de lado 1, por el teorema de Pit¨¢goras sabemos que
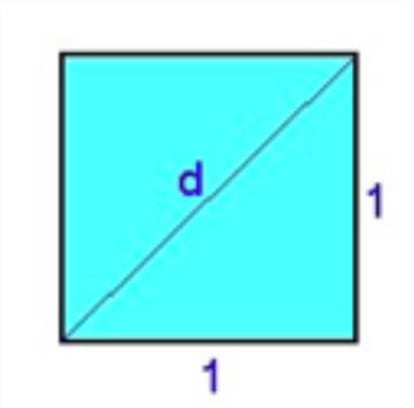
d2 = 12 + 12 = 2
d = ¡Ì2.
Si ¡Ì2 fuera un n¨²mero racional, es decir, una fracci¨®n, podr¨ªamos decir que ¡Ì2 = a/b, donde a y b no son ambos pares (pues en ese caso podr¨ªamos dividirlos ambos por 2 y simplificar la fracci¨®n); por lo tanto:
2 = a2/b2
a2 = 2b2
As¨ª pues, a2 es par, luego a tambi¨¦n lo es (ya que el cuadrado de un n¨²mero impar siempre es impar) y podemos escribirlo en la forma a = 2n (siendo n un n¨²mero entero), de donde a2 = 4n2, y como a2 = 2b2, 2b2 = 4n2, b2 = 2n2, luego b2 es par, lo que significa que b tambi¨¦n lo es, en contra de la hip¨®tesis de partida, seg¨²n la cual a y b no son ambos pares. Por lo tanto, no existe una fracci¨®n a/b que sea igual a ¡Ì2.
Y de forma tan sencilla y elegante demostr¨® Hipaso de Metaponto, hace unos dos mil quinientos a?os, la existencia de los n¨²meros irracionales.
Primos, libros y cuadros
Como hemos visto en las ¨²ltimas semanas, el de los n¨²meros irracionales es un infinito de orden superior al de los n¨²meros naturales, un infinito no numerable (que es una forma de decir que sus elementos no pueden ponerse en correspondencia de uno a uno con el conjunto de los n¨²meros naturales). Pero ?qu¨¦ pasa con los n¨²meros primos, tan escurridizos e inquietantes como los irracionales? Si los irracionales est¨¢n m¨¢s all¨¢ del infinito, ?est¨¢n los primos m¨¢s ac¨¢?
A medida que vamos avanzando en la sucesi¨®n de los n¨²meros naturales, los primos son cada vez m¨¢s escasos; de hecho, podemos encontrar dos primos sucesivos tan alejados como queramos (?puedes demostrarlo?). ?Significa eso que a partir de un cierto punto ya no habr¨¢ m¨¢s n¨²meros primos? Pues no: Euclides, que no solo fue el padre de la geometr¨ªa, sino que tambi¨¦n destac¨® en otras ramas de las matem¨¢ticas, demostr¨® que hay infinitos n¨²meros primos. ?Puedes reconstruir su sencilla e ingeniosa demostraci¨®n?
Y as¨ª como los primos podr¨ªan parecer finitos pero no lo son, hay finitos que no lo parecen, o cuando menos son dudosos. Por ejemplo, se suele decir que el lenguaje es infinito, pero ?lo es realmente? ?Es infinito el n¨²mero de libros escribibles? ?Y el n¨²mero de cuadros pintables?
Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
Sobre la firma


































































