Un Nobel ¡®de plastilina¡¯ para entender el comportamiento de la materia

El Premio Nobel de F¨ªsica 2016 ha sido muy matem¨¢tico (lo cual no est¨¢ mal, ya que en nuestra disciplina no se concede este galard¨®n). Lo han obtenido David J. Thouless, F. Duncan Haldane M. y J. Michael Kosterlitz "por los descubrimientos te¨®ricos de las transiciones de fase topol¨®gicas y fases topol¨®gicas de la materia". En esta especie de trabalenguas se repite la palabra ¡°topolog¨ªa¡±, un ¨¢rea central de las matem¨¢ticas pero muy desconocida para el p¨²blico no matem¨¢tico.

La topolog¨ªa puede entenderse como el estudio de los objetos de plastilina. En vez de estudiar formas r¨ªgidas, se trabaja con objetos deformables. Para hacerse una idea basta acordarse de cuando jug¨¢bamos con plastilina: a partir de una barra, y sin m¨¢s que apretar y aplastar se consiguen diferentes formas: una pelota, un avi¨®n, un cuenco¡­ Las posibilidades son infinitas. Pero, ?y si queremos hacer una taza? ?Ah!, eso es otra cosa. Por m¨¢s que se aplaste o apriete no hay forma de hacer el asa. O bien se pega otro trozo como asa, o bien se rompe el trozo original haciendo un agujero en ¨¦l. Eso s¨ª, una vez hecho el agujero, podemos convertir la taza en una rosquilla o un reloj de pulsera, otra vez estirando, apretando y aplastando. Pero no en unas gafas, que tienen dos agujeros, ni siquiera otra vez en una pelota, que no tiene ninguno.

La topolog¨ªa es la parte de las matem¨¢ticas que estudia las propiedades que quedan invariantes mediante deformaciones que no exigen cortar y pegar

El n¨²mero de agujeros del objeto es una de las propiedades topol¨®gicas m¨¢s sencillas de un trozo de material. La topolog¨ªa es precisamente la parte de las matem¨¢ticas que estudia las propiedades que quedan invariantes mediante deformaciones que no exigen cortar y pegar. Por ser las propiedades que no cambian por deformaciones, son propiedades globales de todo el material. Mirando a un trozo peque?o del mismo (por ejemplo, el interior de la taza) no podemos saber si tendr¨¢ un agujero o no, se necesita una observaci¨®n global del objeto.

Haldane, Kosterlitz y Thouless, en los a?os 70 y 80 se dieron cuenta de que este tipo de propiedades topol¨®gicas interven¨ªan en el comportamiento el¨¦ctrico y magn¨¦tico de materiales en l¨¢minas o filamentos muy finos cuando se enfriaban lo suficiente. Este descubrimiento es el que les ha valido el Premio Nobel en F¨ªsica 2016, concedido por la Real Academia Sueca de Ciencias.

El comportamiento magn¨¦tico de los materiales viene determinado por el esp¨ªn de los electrones, que se puede identificar como un vector (una flecha apuntando en una cierta direcci¨®n). En algunos sistemas, los electrones se encuentran distribuidos uniformemente en un plano y las flechas asociadas a los espines tienen que estar alineadas con el mismo. En este caso pueden aparecer v¨®rtices o remolinos en la distribuci¨®n de los espines. No se pueden crear o destruir cambiando suavemente las direcciones de los espines (como pasaba antes con los agujeros en la plastilina), por lo que son topol¨®gicos.

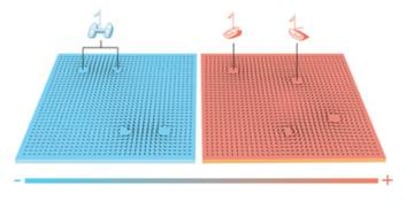
Kosterlitz y Thouless se dieron cuenta de que en ciertos materiales, al modificar la temperatura, el comportamiento de los v¨®rtices cambiaba. Los v¨®rtices pasaban de estar agrupados en pares cercanos con sentido de giro distinto, a estar distribuidos de forma independiente. Este cambio de comportamiento topol¨®gico les permiti¨® explicar la transici¨®n de fase que experimentaba el sistema a cierta temperatura (en el mismo sentido que el hielo y el agua experimentan una transici¨®n de fase a 0 grados), y que no era explicable con las teor¨ªas anteriores.

Haldane aplic¨® t¨¦cnicas similares para estudiar filamentos muy finos a temperaturas cercanas al cero absoluto (-273,15 grados). Usando argumentos topol¨®gicos se dio cuenta de que el comportamiento de los sistemas magn¨¦ticos era radicalmente distinto en funci¨®n de si el n¨²mero de grados de libertad de cada esp¨ªn era par o impar.

Kosterlitz y Thouless se dieron cuenta de que en ciertos materiales, al modificarla temperatura, el comportamiento de los v¨®rtices cambiaba

Desde entonces han aparecido numerosos modelos y materiales cuyo comportamiento s¨®lo puede explicarse utilizando m¨¦todos topol¨®gicos, hasta el punto que el estudio, clasificaci¨®n y s¨ªntesis de los sistemas con propiedades topol¨®gicas se ha convertido en uno de los problemas centrales en la f¨ªsica de los materiales. Adem¨¢s, el car¨¢cter topol¨®gico de estos sistemas los hace muy robustos frente a imperfecciones, ruido y errores, lo que los convierte en firmes candidatos para construir un ordenador cu¨¢ntico en el futuro. En estos ordenadores cu¨¢nticos topol¨®gicos la informaci¨®n se codificar¨ªa y manipular¨ªa en las propiedades topol¨®gicas del material y son numerosas las instituciones y empresas que est¨¢n intentando hacer realidad esta idea que tiene su origen en los trabajos pioneros de Haldane, Kosterlitz y Thouless.

David P¨¦rez Garc¨ªa es profesor de la Universidad Complutense de Madrid y miembro del Instituto de Ciencias Matem¨¢ticas

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.