?Cu¨¢nto llevamos contando?

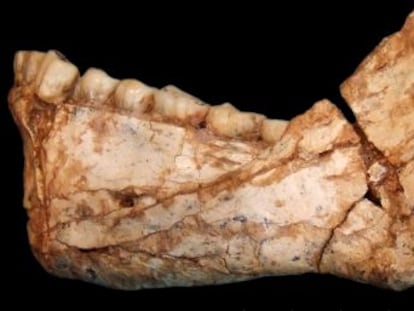
Nuestra cuenta hacia el infinito empez¨® hace varios milenios. De hecho, todo apunta a que el primer pensamiento racional del ser humano consciente estuvo relacionado con contar. Los humanos necesitaban llevar la cuenta del paso del tiempo. Hasta el momento, el rastro m¨¢s antiguo de esa cuenta es un hueso encontrado a principios de la d¨¦cada de 1970 durante una excavaci¨®n en Border Cave, una gruta situada en los montes Lebombo que separan Sud¨¢frica de Suazilandia. Se trata de un fragmento de peron¨¦ de babuino en el que pueden verse 29 muescas claramente definidas. El hueso data aproximadamente del a?o 35.000 a. C., y se cree que ese tipo de hueso se usaba para seguir el paso de los d¨ªas durante un ciclo lunar.

Otro ejemplo m¨¢s sofisticado de cuentas con huesos apareci¨® entre el Congo y Uganda y se conserva ahora en el Real Instituto de Ciencias Naturales de B¨¦lgica. Se lo conoce como el "hueso de Ishango", y los expertos lo fechan en torno al a?o 20.000 a. C. En ¨¦l hay cuatro columnas de muescas, y es evidente que con ellas se contaba algo. En una columna se cuentan 11 muescas, y en las otras 13, 17 y 19. ?Es solo coincidencia que estos sean los n¨²meros primos que hay entre 10 y 20 (lo que de por s¨ª ya es interesant¨ªsimo)? ?O estaba la humanidad ya por entonces obsesionada con esos n¨²meros indivisibles? Lo que est¨¢ claro es que aquellos cavern¨ªcolas se val¨ªan de las muescas para contar algo.

C¨®mo contar hasta infinito

Este texto es un cap¨ªtulo del libro C¨®mo contar hasta infinito (Blackie Books), escrito por el matem¨¢tico Marcus du Sautoy (Londres, 1965). El autor, profesor de matem¨¢ticas en la Universidad de Oxford, es uno de los divulgadores cient¨ªficos brit¨¢nicos m¨¢s populares.

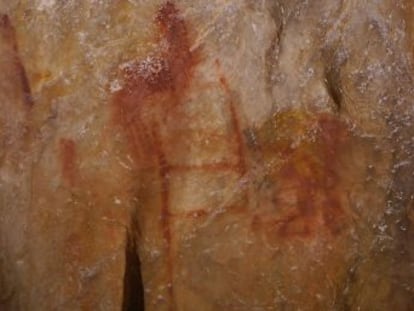
Las pinturas rupestres de Lascaux (15.000 a. C.) dejan tambi¨¦n constancia de aquellas primeras cuentas. En las paredes, junto a las extraordinarias representaciones de animales en movimiento, hay tambi¨¦n extra?as secuencias de puntos. Seg¨²n una de las hip¨®tesis, esos puntos indican los cuartos de la luna. Pueden verse trece puntos que van a dar a un enorme ciervo en plena berrea. Si cada punto refleja un cuarto de la luna, trece puntos comprenden la cuarta parte de un a?o. Una estaci¨®n. La imagen probablemente sea un manual de formaci¨®n para cazadores en ciernes, e indica en qu¨¦ momento del a?o los ciervos est¨¢n en celo y son presa f¨¢cil.

El problema est¨¢ en que contar con puntos o muescas no es un sistema demasiado ¨²til. Para empezar, resulta dif¨ªcil percibir a simple vista cu¨¢ntas muescas tiene el hueso, o cu¨¢ntos puntos hay en la pared. A partir de cinco puntos, los humanos tenemos problemas para distinguir las cantidades que tenemos ante nosotros.

A fin de poder avanzar, diversas culturas de todo el mundo empezaron a desarrollar formas de c¨¢lculo m¨¢s sofisticadas.

Los antiguos egipcios idearon toda una serie de s¨ªmbolos bastante curiosos para indicar que hab¨ªan llegado hasta 10, o hasta 100, o hasta potencias de 10. Para representar el 10 dibujaban un tal¨®n, o una rana para indicar que hab¨ªan llegado a 100.000. El sistema, sin embargo, tampoco iba a ser de mucha ayuda si el objetivo era llegar hasta infinito. A medida que se alcanzaran cifras m¨¢s y m¨¢s altas har¨ªan falta nuevos s¨ªmbolos. En vez de eso, otras culturas descubrieron el poder del sistema de notaci¨®n posicional, mediante el cual es posible intentar contar hasta infinito con un n¨²mero finito de s¨ªmbolos.

Una de esas culturas se encuentra en Am¨¦rica del Sur. Hace ahora unos dos mil a?os, los mayas empezaron a utilizar el sistema de puntos ya empleado por los moradores de las cuevas, pero los mayas, cuando llegaban a cuatro puntos, en lugar de a?adir un quinto hac¨ªan lo que los cautivos cuando llevan la cuenta de d¨ªas que les faltan para salir a la calle: cruzar los cuatro puntos con una l¨ªnea para indicar el 5. Cuando llegaban a 20, en vez de a?adir m¨¢s puntos y m¨¢s l¨ªneas recurr¨ªan a la notaci¨®n posicional de los s¨ªmbolos y a?ad¨ªan una segunda posici¨®n para llevar la cuenta de cu¨¢ntas veintenas llevaban ya. Por ejemplo:

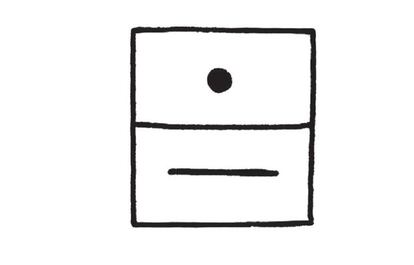
Este diagrama equivale a un bloque de 20 m¨¢s cinco unidades. El contenido de la casilla inferior indica el n¨²mero de unidades (representado en este caso por una l¨ªnea, que son cinco unidades) y el de la casilla superior, el de cantidades de 20 (en este caso, representado por el punto). Ese era su 25. Y as¨ª, solo con puntos y l¨ªneas, pod¨ªan contar hasta infinito. Solo ten¨ªan que a?adir m¨¢s y m¨¢s posiciones para indicar potencias de 20 (del mismo modo que nosotros llevamos la cuenta de las potencias de 10). El sistema de puntos y rayas de los mayas era muy sofisticado, a tal punto que permit¨ªa a los astr¨®nomos mantener un registro de extens¨ªsimos per¨ªodos de tiempo.

Este sistema de notaci¨®n posicional ya lo emple¨® una de las primeras culturas en practicar las matem¨¢ticas. Los antiguos babilonios contaban en m¨²ltiplos de 60. Ten¨ªan s¨ªmbolos que llegaban hasta 59, y a continuaci¨®n abr¨ªan una nueva columna para indicar la cuenta de otro bloque de 60. Llegados a este punto, estoy seguro de que os pregunt¨¢is por qu¨¦ contamos en grupos de 10 mientras otras culturas lo hacen en grupos de 20 o 60. Si optamos por el sistema decimal no fue porque el 10 tuviese una importancia matem¨¢tica especial, sino simplemente porque cont¨¢bamos con las manos. Los Simpson, que tienen ocho dedos, seguramente cuentan en secuencias de 8. Quiz¨¢ los mayas contaban en grupos de 20 porque usaban las manos y los pies.

Entonces, ?por qu¨¦ contaban los babilonios en grupos de 60? Una raz¨®n a tener en cuenta est¨¢ en las propiedades matem¨¢ticas especiales de esa cifra. Es un n¨²mero altamente divisible. Puede dividirse entre 2, 3, 4, 5, 6, 10, 12, 15 y 30, y eso lo hace muy flexible. Pero hay otra teor¨ªa, seg¨²n la cual el 60 guarda relaci¨®n con nuestra anatom¨ªa. Existe una manera de contar hasta 60 con los huesos de las manos. Tenemos 12 huesos en cuatro dedos de la mano derecha. Usando el pulgar podemos contar del 1 al 12. Con los dedos de la mano izquierda llevamos la cuenta de cu¨¢ntos doces llevamos contados. Podemos contar hasta cinco grupos de 12..., es decir, hasta 60.

Aunque hoy contamos de diez en diez, a¨²n quedan reductos del sistema sexagesimal babilonio en la forma en que registramos el paso del tiempo. Un minuto tiene 60 segundos. Una hora, 60 minutos.

Y ahora que tenemos s¨ªmbolos diferenciados para llevar la cuenta de nuestro avance hacia el infinito, necesitamos una estrategia para llegar hasta ¨¦l.