Porque 70 millones ¡°no son nada¡±

Los n¨²meros primos, n¨²meros que solamente tienen dos divisores distintos (el 1 y el propio n¨²mero), siguen encerrando multitud de misterios a¨²n fuera del alcance del ser humano, sea matem¨¢tico o no. Este conjunto num¨¦rico, ¡°generador¡± de todos los n¨²meros naturales, sigue a d¨ªa de hoy escondiendo las respuestas a una gran cantidad de preguntas que matem¨¢ticos de todas las ¨¦pocas se han hecho sobre ellos.

Entre todas ellas, hay una muy conocida que a m¨ª particularmente me encanta: ?existen infinitas parejas de primos gemelos? Dos n¨²meros primos son primos gemelos si hay una distancia de dos unidades entre ellos. Por ejemplo, 3 y 5 son primos gemelos; 17 y 19 tambi¨¦n; y tambi¨¦n lo son 521 y 523. Lo que todav¨ªa no se sabe es si llega un momento en el que dichas parejas dejan de aparecer, o si por el contrario podemos encontrar parejas de primos de estas caracter¨ªsticas ad infinitum.

Esta conjetura de los primos gemelos lleva en boca y en mente de matem¨¢ticos desde hace m¨¢s de 2000 a?os, y, como dec¨ªamos antes, en la actualidad sigue sin respuesta. Es cierto que hay resultados que refuerzan la idea de que hay infinitas parejas de este tipo, y que la comunidad matem¨¢tica cree que as¨ª es, pero seguimos sin demostraci¨®n hacia uno u otro lado.

Bien, pues hace cinco a?os, en 2013, el matem¨¢tico Yitang Zhang presentaba un resultado relacionado con esta conjetura que sorprendi¨® enormemente a matem¨¢ticos de uno y otro lado. En su trabajo, Bounded gaps between primes, Zhang demostraba el siguiente resultado:

¡°Existen infinitas parejas de n¨²meros primos que est¨¢n a una distancia menor de 70.000.000.¡±

S¨ª, 70 millones, nada m¨¢s y nada menos.

Cuando un lee esto, la pregunta es casi inmediata: ?70 millones? ?Y qu¨¦ avance es ese? Y lo entiendo. Una distancia de 70 millones de unidades es tan grande para cualquiera que es complicado comprender qu¨¦ ventaja o beneficio puede tener, pero lo tiene.

Hasta ese momento, no se dispon¨ªa de un resultado de ese tipo. Es decir, no se sab¨ªa si hab¨ªa infinitas parejas de n¨²meros primos que estuvieran a una distancia menor que un cierto n¨²mero. Este teorema de Zhang daba un punto de partida: ya sabemos que hay infinitas parejas de primos a distancia menor que 70 millones, afinemos ahora el resultado para intentar llegar a distancia menor que 3 y tendremos demostrada la conjetura de los primos gemelos.

M¨¢s informaci¨®n

Desmontando (una vez m¨¢s) los absurdos sorteos por letra

La madre de los enunciados f¨¢cil-dif¨ªcil

?Por qu¨¦ 3435 es uno de mis n¨²meros favoritos?

Al parecer, esa ¡°cota¡± de 70.000.000 era f¨¢cilmente mejorable a partir del propio trabajo de Zhang, y multitud de matem¨¢ticos de todo el mundo se lanzaron a ello tras la publicaci¨®n de este trabajo: en unos d¨ªas se hab¨ªa bajado a 6 millones; m¨¢s tarde, el genial matem¨¢tico australiano Terence Tao abri¨® un polymath (proyecto colaborativo donde matem¨¢ticos de todo el mundo trabajan conjuntamente y se comunican online) con el cual la cota se rebaj¨® a menos de 5000; y despu¨¦s, gracias a los avances hechos por James Maynard, se lleg¨® a 700. En unos seis meses se hab¨ªa bajado de 70000000 a 700, un progreso considerable.

El trabajo de Maynard, Small gaps between primes, anim¨® a los participantes del polymath citado antes y propici¨® que dicha cota se bajara hasta 246 (hab¨ªa pasado solamente un a?o desde los famosos 70 millones)¡­pero por desgracia ah¨ª nos hemos quedado. Todos los expertos est¨¢n de acuerdo en que estos trabajos no conseguir¨¢n rebajar la cota a 3, por lo que hacen falta ideas nuevas para atacar la conjetura de los primos gemelos. Por tanto, y a pesar del valioso trabajo de Yitang Zhang, la conjetura de los primos gemelos sigue sin respuesta. Fue bonito mientras dur¨®, pero parece que por ah¨ª no podremos avanzar m¨¢s.

Pero los resultados relacionados con los primos gemelos no acaban ah¨ª, ni mucho menos. A principios del pasado siglo XX, concretamente en 1919, el matem¨¢tico noruego Viggo Brun demostraba un resultado que, en cierta forma, ¡°choca¡± con la creencia de la existencia de infinitas parejas de primos gemelos.

Para cada pareja de primos gemelos, Brun consider¨® la suma de los inversos de los dos n¨²meros de la pareja. Por ejemplo, para la pareja (3,5), Brun toma 1/3+1/5; para (5,7), tendr¨ªamos 1/5+1/7; y as¨ª sucesivamente. Despu¨¦s Brun consider¨® la suma de todos los resultados, suponiendo (como no pod¨ªa ser de otra forma) que hay infinitas parejas de primos gemelos (para los ya iniciados, puede que esta explicaci¨®n sea demasiado simple y carente de rigor, pero no he encontrado otra forma mejor de explicarlo a nivel usuario).

Tenemos entonces la siguiente suma infinita:

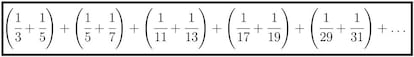
Si pudi¨¦ramos calcular el valor de dicha suma y el resultado fuera infinito, la conjetura de los primos gemelos ya estar¨ªa demostrada (si el resultado de la suma es infinito, entonces obligatoriamente hay infinitos n¨²meros involucrados). Pero lo que demostr¨® Brun es que esa suma infinita tiene como resultado un n¨²mero real, y adem¨¢s bastante peque?o (no llega a 2). M¨¢s concretamente, la mejor aproximaci¨®n de la que disponemos actualmente sobre esta constante de Brun data de 2002, y es la siguiente:

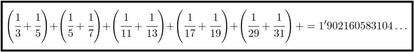
Un resultado maravilloso este de Brun, que unido a los trabajos de Zhang, Tao, Maynard y compa?¨ªa seguro que conseguir¨¢n que muchos se enamoren de esta conjetura de los primos gemelos (si no lo estaban ya). Lo malo de todo esto es que la conjetura sigue sin soluci¨®n, por lo que a¨²n estamos sin respuesta; lo bueno, que la conjetura sigue sin soluci¨®n, por lo que todav¨ªa podemos disfrutar con ella.

Para finalizar, un apunte. Es posible que m¨¢s de uno se haya asombrado al leer que hay sumas de infinitos n¨²meros cuyo ¡°resultado¡± no es infinito, sino un n¨²mero real concreto. Pues s¨ª, las matem¨¢ticas son as¨ª de maravillosas y nos traen cuestiones tan sorprendentes como esta. Dejaremos para pr¨®ximos art¨ªculos una explicaci¨®n algo m¨¢s profunda de este asunto.