Curvas y curvaturas

Hay espadas de todos los tama?os y de las formas m¨¢s variadas; pero no es casual que, como ve¨ªamos la semana pasada, la mayor¨ªa de las veces sus hojas sean rectas o arcos de circunferencia, y una de las razones es porque solo estos dos tipos de hojas pueden envainarse. La circunferencia es la ¨²nica curva plana con una curvatura uniforme, por lo que un arco de circunferencia puede deslizarse por toda ella. Y una recta tambi¨¦n tiene una curvatura uniforme -curvatura nula- y un segmento puede deslizarse por toda su longitud. Hay una tercera curva que puede ¡°envainarse¡±, pero no es plana: la h¨¦lice cil¨ªndrica (el t¨ªpico muelle) y no parece muy adecuada para dar forma a la hoja de una espada.

Decir que una recta tiene una curvatura nula es algo que, intuitivamente, tiene sentido, puesto que no est¨¢ nada curvada; pero ?qu¨¦ se entiende exactamente por curvatura y c¨®mo se cuantifica? En primer lugar, hay que tener en cuenta que la curvatura se define en cada punto, no es una propiedad general de toda la curva, salvo en el caso de la circunferencia (de momento nos limitaremos a las curvas planas). En una elipse, por ejemplo, es evidente que en los extremos del eje mayor la curvatura es m¨¢s acentuada que en los del eje menor.

Una definici¨®n rigurosa de la curvatura exige echar mano del c¨¢lculo diferencial (cosa que no haremos aqu¨ª, y menos en agosto); pero, siguiendo a Arqu¨ªmedes, podemos dividir una curva cualquiera en diminutos fragmentos consecutivos y considerar que cada uno de ellos es un arco de circunferencia (es un ¡°truco¡± parecido al de considerar que un c¨ªrculo es un pol¨ªgono de infinitos lados); pues bien, el radio de curvatura en cada punto es el radio de la circunferencia que mejor se ajusta a la curva en ese punto, y la curvatura, que se suele expresar con la letra k, se define como el inverso de ese radio: k = 1/r.

Huevos y ovoides

El ovoide (denominado as¨ª porque parece la secci¨®n longitudinal de un huevo) constituye un caso sencillo, puesto que no est¨¢ formado por arcos de circunferencia infinitesimales, sino por cuatro muy concretos y visibles: una semicircunferencia en la base, dos amplios arcos laterales sim¨¦tricos y un peque?o arco m¨¢s cerrado en la punta.

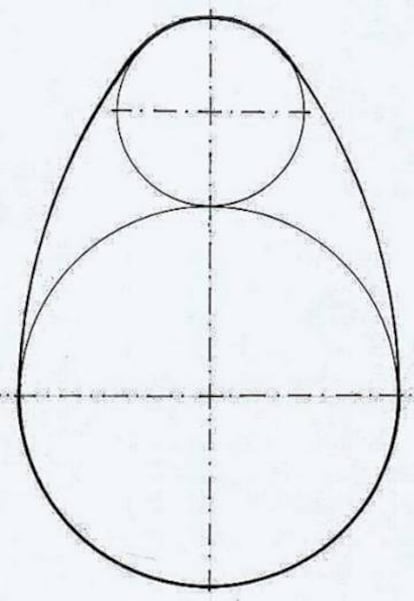
Si tomamos como unidad el radio de la semicircunferencia de la base, ?cu¨¢l es la curvatura de las distintas partes del ovoide? Tal como muestra la figura, los extremos del di¨¢metro de la semicircunferencia de la base (que es el eje menor del ovoide) son los centros de los arcos laterales. Con esta informaci¨®n, ?c¨®mo podemos dibujar un ovoide, con regla y comp¨¢s, dado su eje menor?

Y pasando de la matem¨¢tica a la f¨ªsica y de la f¨ªsica a la biolog¨ªa, ?por qu¨¦ la mayor¨ªa de los huevos son ovoides (valga la perogrullada)? ?No ser¨ªa mejor que fueran redondos? A igual volumen, la esfera tiene una superficie menor, por lo que supone un menor consumo de calcio para generar la c¨¢scara, y a la vez es m¨¢s resistente. Y sin embargo¡­

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellosMaldita f¨ªsica,Malditas matem¨¢ticasoEl gran juego. Fue guionista deLa bola de cristal.