?Pueden aprender matem¨¢ticas los insectos?
Un grupo de investigadores 'ense?a' a una colmena de abejas a sumar y restar

La revista Science Advances publica hoy los resultados de una investigaci¨®n que muestra que las abejas europeas son capaces de usar representaciones simb¨®licas para resolver operaciones matem¨¢ticas simples como sumas y restas.
A pesar de poseer un cerebro con poco menos de un mill¨®n de neuronas, estos insectos son capaces de resolver problemas complejos como la comprensi¨®n del concepto de cero.
Las abejas son un gran modelo para investigar en neurociencia. Por eso en nuestro mas reciente experimento decidimos probar la capacidad de este insecto para resolver operaciones aritm¨¦ticas simples.
Sumas y restas
De ni?os aprendemos que el s¨ªmbolo m¨¢s (+) significa que debemos sumar dos o m¨¢s cantidades, mientras que el s¨ªmbolo menos (-) indica que debemos sustraerlas. Para resolver este tipo de problemas, necesitamos usar nuestra memoria a corto y a largo plazo. Una vez hemos aprendido y almacenado las reglas de adici¨®n y sustracci¨®n en nuestra memoria a largo plazo, la memoria a corto plazo nos permite manejar las cantidades involucradas en cada operaci¨®n que realizamos.
A pesar de que no es f¨¢cil resolver operaciones aritm¨¦ticas como sumar y restar, esta habilidad ha sido fundamental para las sociedades humanas. Por ejemplo, la evidencia arqueol¨®gica muestra que los egipcios y babilonios ya usaban operaciones aritm¨¦ticas alrededor del a?o 2000 a.C.. Estas habr¨ªan sido ¨²tiles para contar ganado y recalcular el n¨²mero de cabezas restantes despu¨¦s de una venta.
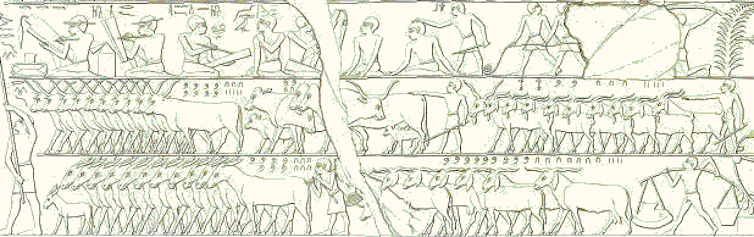 La escena (copiada por el egipt¨®logo Lepsius) muestra un grupo de escribas contando cabezas de ganado. En la segunda fila podemos observar 835 cabezas a la izquierda, y alrededor de 2235 cabras a la derecha. En la fila inferior se pueden observar 760 asnos a la izquierda y 974 cabras a la derecha.?/?Wikicommons
La escena (copiada por el egipt¨®logo Lepsius) muestra un grupo de escribas contando cabezas de ganado. En la segunda fila podemos observar 835 cabezas a la izquierda, y alrededor de 2235 cabras a la derecha. En la fila inferior se pueden observar 760 asnos a la izquierda y 974 cabras a la derecha.?/?Wikicommons
Uno podr¨ªa preguntarse si el desarrollo del pensamiento aritm¨¦tico requiere un cerebro tan grande como el que poseemos los primates o si otros animales tambi¨¦n son capaces de realizar operaciones aritm¨¦ticas cuando se enfrentan a problemas similares. Hemos intentado responder a esa pregunta usando como modelo a la abeja europea.
?C¨®mo se entrena una abeja?
Las abejas son forrajeadoras centrales, lo que significa que una obrera volver¨¢ al mismo sitio siempre y cuando exista una fuente de alimento. Usamos una soluci¨®n concentrada de az¨²car durante todo el experimento para asegurarnos que regresaran de manera contin¨²a.
Cada vez que una abeja escog¨ªa el n¨²mero correcto (ver detalles m¨¢s adelante) recib¨ªa una recompensa de agua azucarada. Por el contrario, si la abeja realizaba una elecci¨®n equivocada, recib¨ªa un castigo en forma de una soluci¨®n amarga hecha a base de quinina.
En nuestro experimento utilizamos este sencillo m¨¦todo para ense?ar a las abejas a sumar o restar durante sesiones de cuatro a siete horas por individuo. Cada vez que una abeja se saciaba con la soluci¨®n azucarada, regresaba a la colmena y m¨¢s tarde volv¨ªa para continuar con el entrenamiento.
Adici¨®n y sustracci¨®n en abejas
Las abejas fueron entrenadas de manera individual con un laberinto en forma de Y (ver figura abajo). Durante el experimento, los insectos volaban hasta la entrada, donde ve¨ªan un grupo de entre uno y cinco elementos. Estos representaban formas geom¨¦tricas (por ejemplo, un cuadrado) que pod¨ªan ser de dos colores diferentes seg¨²n la operaci¨®n aritm¨¦tica a entrenar: azul para sumar un elemento (+ 1) o amarillo para restarlo (- 1).
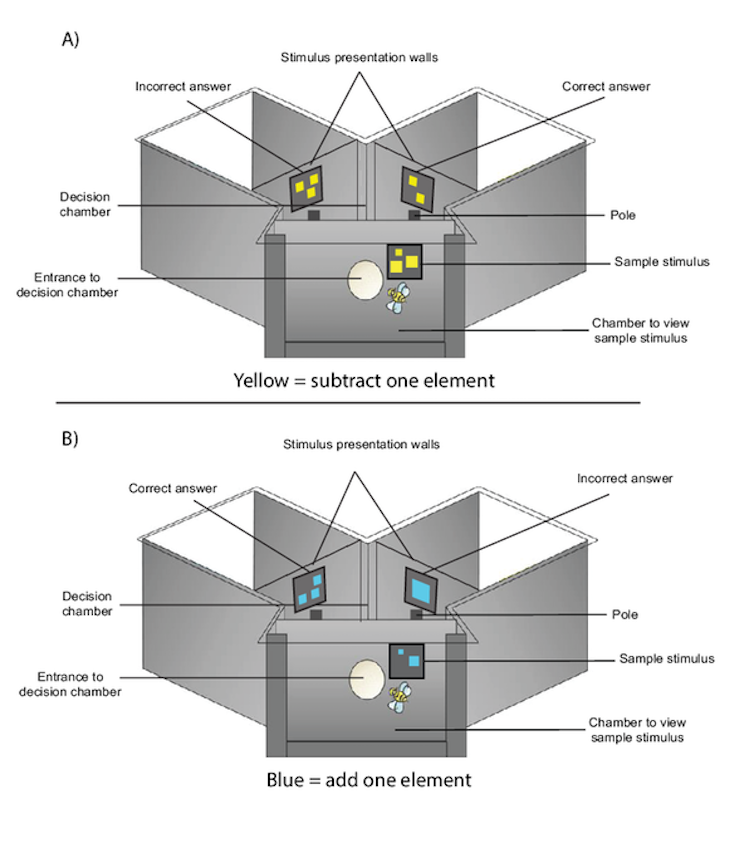 Laberinto en forma de Y usado para entrenar a las abejas.?/?Scarlett Howard
Laberinto en forma de Y usado para entrenar a las abejas.?/?Scarlett Howard
A partir de esta informaci¨®n, la abeja ten¨ªa que volar a trav¨¦s de un orificio hacia la c¨¢mara de decisiones, donde deb¨ªa escoger uno de los brazos del laberinto. Un brazo conten¨ªa un elemento m¨¢s del visto en la entrada y el otro uno menos. En cada ronda del experimento el animal ten¨ªa que escoger el brazo hacia el cual deber¨ªa volar seg¨²n el n¨²mero inicial de objetos vistos a la entrada y la operaci¨®n para la cual estaba siendo entrenada.
La posici¨®n del grupo correcto se cambiaba aleatoriamente en el laberinto, para evitar que las abejas relacionaran uno de los lados con la respuesta correcta. Al comienzo del experimento, las abejas escog¨ªan al azar el brazo del laberinto al cual se dirig¨ªan. Despu¨¦s de cien ensayos aprendieron a escoger la soluci¨®n correcta al problema.
Al terminar el entrenamiento, les presentamos a las abejas un n¨²mero de elementos que nunca hab¨ªan visto. Las abejas escogieron la respuesta correcta entre el 64 y el 72 % de las veces. Esta proporci¨®n es estad¨ªsticamente diferente a lo que se esperar¨ªa si hubieran elegido las respuestas al azar. Por lo tanto, los insectos de nuestra escuela de abejas aprendieron a usar operadores aritm¨¦ticos para sumar y restar.
?Por qu¨¦ es esto dif¨ªcil para las abejas?
Sumar y restar es dif¨ªcil porque requiere procesar la informaci¨®n a dos niveles y de manera simult¨¢nea. Por un lado, la comprensi¨®n de los atributos num¨¦ricos; por el otro, su manipulaci¨®n para operar.
Las abejas tambi¨¦n usaron su memoria a corto plazo. Como el n¨²mero 1 a ser sumado o restado no estaba presente al realizar la operaci¨®n, los insectos tuvieron que aprender este concepto abstracto durante el entrenamiento.
Al demostrar que las abejas pueden combinar un aprendizaje aritm¨¦tico y simb¨®lico simple, identificamos nuevas ¨¢reas del conocimiento para explorar, como, por ejemplo, la capacidad de otros animales para sumar o restar.
Inteligencia artificial y neurobiolog¨ªa
La inteligencia artificial y c¨®mo los ordenadores pueden aprender a resolver nuevos problemas de manera aut¨®noma son dos temas de gran inter¨¦s en la actualidad.
Nuestros descubrimientos muestran que cerebros peque?os son capaces de aprender operadores aritm¨¦ticos simb¨®licos, lo que sugiere nuevas maneras de incorporar interacciones entre la memoria a corto y largo plazo, para as¨ª reducir los tiempos de aprendizaje en los sistemas de inteligencia artificial.
Asimismo, nuestros resultados demuestran que hay varias maneras de entender los s¨ªmbolos matem¨¢ticos como un lenguaje de operadores. Esto podr¨ªa ayudar a entender c¨®mo diferentes culturas desarrollaron de manera independiente habilidades num¨¦ricas.
Este art¨ªculo ha sido publicado simult¨¢neamente en ingl¨¦s.![]()
Scarlett Howard, PhD candidate, RMIT University; Adrian Dyer, Associate Professor, RMIT University y Jair Garcia, Research fellow, RMIT University
Este art¨ªculo fue publicado originalmente en The Conversation. Lea el original.
![]()
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.






























































