Matem¨¢ticamente cotidiano

En la entrada anterior tuvimos ocasi¨®n de conocer el planteamiento que sosten¨ªa Jos¨¦ Pedro Mart¨ªn, profesor de matem¨¢ticas del?Instituto P¨²blico de Educaci¨®n Secundaria Obligatoria (IESO) ¡®V¨ªa Dalmacia¡¯ de Torrejoncillo en C¨¢ceres.

Afirmaba que las matem¨¢ticas aportan otra mirada de lo cotidiano, con la que contribuye a dotarlo de mayor sentido.

©¤ Jos¨¦ Pedro Mart¨ªn: ¡°Las matem¨¢ticas no son un ente est¨¢tico y apartado que se estudia de forma aut¨®noma, sino ¡®algo¡¯ muy importante que forma parte de un ¡®todo¡¯, que es la vida de cada uno de nosotros y que, con toda seguridad, los alumnos las van a necesitar a lo largo de la vida. Les ayudar¨¢n a ser m¨¢s independientes, m¨¢s cr¨ªticos... y, en definitiva, m¨¢s libres.¡±

La experiencia a la que nos referimos se denomina Phytagoras' Game y se despleg¨®, en el curso 2017/18, con estudiantes de Segundo de Educaci¨®n Secundaria Obligatoria (ESO). Una tentativa poco frecuente de organizar la ense?anza y el aprendizaje del Teorema de Pit¨¢goras y de su aplicaci¨®n al c¨¢lculo de ¨¢reas y per¨ªmetros de figuras planas.

©¤ Raquel (estudiante): "En la actividad de fotograf¨ªa matem¨¢tica, no me imaginaba que en la calle pod¨ªa encontrar tri¨¢ngulos rect¨¢ngulos y aplicar el Teorema de Pit¨¢goras. A veces, se necesita mucha imaginaci¨®n...¡±

La educaci¨®n matem¨¢tica, como concepto y pr¨¢ctica cada vez m¨¢s evolucionados, pretende la formaci¨®n de los estudiantes para poder... ¡°analizar, razonar y comunicar efectivamente mientras que plantean, resuelven e interpretan problemas en una variedad de situaciones que implican diferentes conceptos matem¨¢ticos como los cuantitativos, espaciales, probabil¨ªsticos, entre otros¡± (OCDE, 2003: 24). Su sentido no se encontrar¨ªa, por tanto, en la capacitaci¨®n para el ejercicio profesional de las matem¨¢ticas, sino en la formaci¨®n para el desarrollo de habilidades de comprensi¨®n matem¨¢tica, de resoluci¨®n de problemas complejos, desconocidos y no rutinarios, y de toma de decisiones basada en informaci¨®n cuantitativa.

Las matem¨¢ticas necesitan prop¨®sitos de mucho calado, en su integraci¨®n curricular y en los m¨¦todos de ense?anza. Es preciso indagar nuevas referencias, alternativas metodol¨®gicas... centradas en una educaci¨®n en ¡®profundidad¡¯, desde las que asegurar el dominio de determinadas habilidades de compresi¨®n y aplicaci¨®n, el contagio de buenas actitudes y el aumento de las expectativas de ¨¦xito en el abordaje de las tareas matem¨¢ticas. En el aprendizaje de las matem¨¢ticas se hace ineludible la utilizaci¨®n sistem¨¢tica de procesos de planificaci¨®n, control y reflexi¨®n individual y colectiva.

La educaci¨®n matem¨¢tica debe huir del planteamiento, demasiado habitual, de muchos manuales escolares y ¡®cuadernos de ejercicios¡¯ que presentan una materia centrada en problemas rutinarios, basados en la aplicaci¨®n de algoritmos prefabricados y con poca capacidad para despertar ¡®inter¨¦s¡¯ entre los estudiantes. Las matem¨¢ticas necesitan liberarse de la etiqueta de asignatura-obst¨¢culo para el progreso acad¨¦mico y de aprendizaje de los estudiantes. De malditas a deseadas, ser¨ªa el lema que debe presidir la configuraci¨®n de cualquier entorno de aprendizaje sobre las matem¨¢ticas.

?stas son las referencias adoptadas en la creaci¨®n del ¡®escenario de aprendizaje¡¯, secuenciado y sustentado virtualmente, que vino a denominarse: Phytagoras' Game.

La secuencia de desarrollo de este escenario comienza con la presentaci¨®n de las bases de trabajo, en una sesi¨®n inicial, donde se enuncian, tambi¨¦n, los componentes estructurales y funcionales del proyecto. Entre otros, la organizaci¨®n de los equipos de trabajo, al buen uso del blog de cada equipo y de las cuentas de correo electr¨®nico, la creaci¨®n del correspondiente avatar del grupo... A partir de este momento, se crearon las bit¨¢coras de ¡°Hipotenusa al Cuadrado¡±, ¡°Los pent¨¢gonos¡±, ¡°Suicide Squad¡±, ¡°V¨ªctor and Company 2?A¡±y ¡°Los Poliedros¡±.

Despu¨¦s de estos previos, esta unidad de aprendizaje contempla todo un conjunto de tareas y actividades.Unas se abordan individualmente, otras en pareja, formando tr¨ªos o en peque?o grupo.

Tareas

A tenor del tipo de actividades y del objetivo pretendido (la compresi¨®n y aplicaci¨®ndel Teorema de Pit¨¢goras en el c¨¢lculo de ¨¢reas y per¨ªmetros de figuras planas) se articulan distintas actividades y tareas; si bien, sus componentes estructurales se mantienen y, adem¨¢s, con el mismo orden: Descripci¨®n de la tarea, desarrollo y modalidad de realizaci¨®n (individual, parejas, tr¨ªo o peque?o grupo), puntuaci¨®n asignada y r¨²brica de evaluaci¨®n.

Las r¨²bricas espec¨ªficas de cada tarea act¨²an como gu¨ªas de autoevaluaci¨®n individual y grupal y ejercen un papel regulador del aprendizaje.

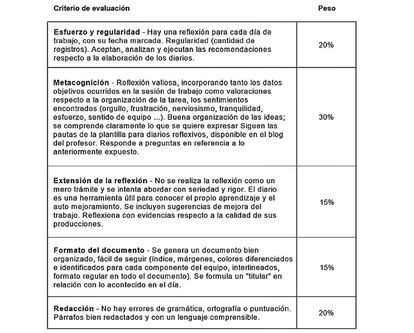
A modo de ejemplo, facilitamos a continuaci¨®n la r¨²brica utilizada en la tarea: Diario de aprendizaje. En este caso, elaborada por Francisco Jes¨²s Montero y disponible, junto a la correspondiente descripci¨®n y argumentaci¨®n de buen uso, en la entrada de la web del Cedec (Centro Nacional de Desarrollo Curricular en Sistemas no Propietarios): Los diarios de aprendizaje, una herramienta para reflexionar sobre el propio aprendizaje.

La unidad tem¨¢tica Phytagoras' Game se estructura en nueve tareas: (1) Diario de aprendizaje, (2) V¨ªdeo sobre Pit¨¢goras, (3) Ternas pitag¨®ricas, (4) ?reas y per¨ªmetros de figuras planas, (5) Fotograf¨ªa matem¨¢tica, (6) Resoluci¨®n de problemas por parejas,(7) Circuito matem¨¢tico, (8) Presentaci¨®n de la unidad a los compa?eros y compa?eras y (9) Prueba individual.

A continuaci¨®n, ilustramos algunas de ellas, en raz¨®n a las sugerencias pr¨¢cticas que ofrecen y las posibilidades de generalizaci¨®n.

Diario de aprendizaje

Con esta tarea se pretende que cada estudiante escriba en un espacio virtual, utilizando un editor, tambi¨¦n virtual, un documento-diario, del que se informa al grupo y comparte. En el diario debe reflejar, al final de la tarea, el modo de enfrentarse a la resoluci¨®n de las actividades que contempla, as¨ª como, sus impresiones, aprendizajes logrados... y, en su caso, un titular que represente y resuma los aspectos b¨¢sicos que se desean destacar.

La r¨²brica incorporada en p¨¢rrafos anteriores ofrece informaci¨®n sobre el peso de los distintos criterios aplicados en la evaluaci¨®n de cada diario de aprendizaje.

V¨ªdeo sobre Pit¨¢goras

Los estudiantes suelen mostrar bastante destreza en el uso del tel¨¦fono m¨®vil y las apps descargables. La gran mayor¨ªa manejan la c¨¢mara y las aplicaciones relacionadas con la edici¨®n y la mejora del visionado de v¨ªdeos. La idea, en este caso, ser¨ªa aprovechar este dominio ¡ªen lugar de prohibir su uso¡ª, dar rienda suelta a su creatividad y ponerlo en relaci¨®n con un contenido de aprendizaje escolar: el Teorema de Pit¨¢goras.

©¤ Jos¨¦ Pedro Mart¨ªn: ¡°Considero que en nuestras aulas no se les da la oportunidad para expresar lo que llevan dentro. Muchos de ellos a¨²n no lo han descubierto porque ni siguiera lo han intentado. Por eso pienso que son de suma importancia este tipo de tareas.¡±

?sta ser¨ªa la primera planteada a realizar en equipo y consiste en montar un v¨ªdeo, de no m¨¢s de cinco minutos de duraci¨®n, en el que relatar¨¢n qui¨¦n fue Pit¨¢goras y qu¨¦ conocen sobre el teorema que lleva su nombre.

Investigar, guionizar, interpretar, grabar, editar, subir el v¨ªdeo a la plataforma¡­ son aprendizajes ¨²tiles que, adem¨¢s del acercamiento al Teorema de Pit¨¢goras, se ponen en juego, en esta tarea y, de esta manera, conseguir trabajar muchas de las competencias formuladas en el curr¨ªculo oficial.

©¤ Arturo (estudiante): "La actividad que m¨¢s me gust¨® fue la elaboraci¨®n del v¨ªdeo, adem¨¢s de compartir experiencias con otros compa?eros, me un¨ª mucho a Diego, un compa?ero de clase al que apenas conoc¨ªa, y cre¨¦ amistad con ¨¦l. Adem¨¢s de pasar un momento divertido, aprendimos mucho a montar un v¨ªdeo".

Fotograf¨ªa matem¨¢tica

Las matem¨¢ticas est¨¢n muy presentes en la vida diaria y en el arte. Esta consideraci¨®n suele estar lejos de las aulas y llega a muy pocos alumnos. Con esta tarea se pretende hacer patente que los tri¨¢ngulos rect¨¢ngulos y, por tanto, el Teorema de Pit¨¢goras est¨¢ presente en muchos elementos arquitect¨®nicos, art¨ªsticos, etc. Los estudiantes pueden observar esta circunstancia nada m¨¢s salir a la calle.

Para su realizaci¨®n buscaron en su entorno motivos matem¨¢ticos en los fuese de aplicaci¨®n el Teorema de Pit¨¢goras.

Para profundizar en las posibilidades did¨¢cticas de este tipo de tareas, recomendamos visitar la web del Grupo de Docentes de Matem¨¢ticas: Enfoque geom¨¦trico.

Circuito matem¨¢tico

Como una extensi¨®n de la tarea anterior surge otra con mayor relevancia (que ya comentamos en el ¡®post¡¯ anterior), donde se muestra la aplicabilidad cotidiana del conocimiento matem¨¢tico.

Se hace necesario desarrollar la habilidad de los estudiantes para enfrentarse exitosamente a contextos variados que les exigen aplicar los conocimientos matem¨¢ticos que poseen.

_{^{Aportes para la ense?anza de la matem¨¢tica.
UNESCO. 2016}}

En esta prueba, por tr¨ªos, se les entrega un dossier con problemas propuestos y un plano donde est¨¢n ubicadas las figuras geom¨¦tricas. Los estudiantes deben acudir a los lugares marcados, tomar las medidas indicadas y cuantificar ¨¢reas y per¨ªmetros de las figuras geom¨¦tricas localizadas, todo en un tiempo de hora y media.

©¤ Jos¨¦ Pedro Mart¨ªn: ¡°Quiz¨¢s fue ¨¦ste el principal objetivo que nos planteamos antes de empezar la unidad, poner en pr¨¢ctica los conocimientos adquiridos. Por eso la resoluci¨®n de problemas en la calle, la aplicaci¨®n de lo aprendido para resolver dudas que se les planteen en una fachada, una cornisa, una puerta... y distinguir elementos geom¨¦tricos que nos encontramos d¨ªa a d¨ªa sea el prop¨®sito de todo nuestro trabajo.¡±

Esta tarea en la actualidad cuenta con cierta tradici¨®n entre el profesorado de matem¨¢ticas. Valga de referencia el siguiente ¡®clip¡¯ de v¨ªdeo del Telediario (15 horas - 17/04/19) de La 1 de TVE, haci¨¦ndose eco de la labor y prop¨®sitos de los ¡®Paseos Matem¨¢ticos¡¯.

Otras tareas y actividades tuvieron lugar en este nuevo escenario de aprendizaje. A continuaci¨®n, mostramos algunas im¨¢genes sobre la tarea: Ternas pitag¨®ricas.

^{La terna pitag¨®rica | Jos¨¦ Pedro Mart¨ªn Lorenzo}

Presentaci¨®n de la unidad

Esta categor¨ªa de aprendizajes consist¨ªa en la elaboraci¨®n de una presentaci¨®n en la que resumir el trabajo llevado a cabo en esta unidad. La exposici¨®n y defensa se hac¨ªa por cada equipo, en clase, ante el resto de los compa?eros y las compa?eras, y contaban con la participaci¨®n de todos los componentes del equipo.

Evaluaci¨®n y calificaci¨®n de los aprendizajes

©¤ Jos¨¦ Pedro Mart¨ªn: ¡°El trabajo con los chicos en l¨ªneas generales fue muy din¨¢mico y participativo; ellos aportaban sus opiniones, quejas e impresiones a lo largo de la unidad y eso me serv¨ªa a m¨ª como elemento de evaluaci¨®n del proceso.¡±

El nivel de logro de cada tarea iba arrojando puntuaciones para cada equipo y para cada estudiante. Cada alumno y cada alumna obten¨ªa una calificaci¨®n individual de forma proporcional al nivel de desarrollo y logro de la tarea grupal. Aquellas otras puntuaciones conseguidas de forma individual se aportaban, a su vez, a la calificaci¨®n del equipo, utilizando una serie de algoritmos.

Difusi¨®n de la unidad

La experiencia, adem¨¢s de ser publicada en el blog de clase (El Club de los N¨²meros), tambi¨¦n lo fue en la web de Cedec con el t¨ªtulo Pit¨¢goras en una Unidad Gamificada. Una experiencia del Club de los N¨²meros.A ra¨ªz de ello, Jos¨¦ Pedro recibi¨® la propuesta de crear un Recurso Educativo Abierto (REA) dentro del Proyecto EDIA,que lidera tambi¨¦n el Cedec.

Tambi¨¦n se expuso la unidad en las II Jornadas ¡®Ondas San Jos¨¦¡¯ para la mejora de las competencias comunicativas en Villanueva de la Serena (Badajoz). Adem¨¢s, ha sido compartida por redes socialesy abriga el prop¨®sito de que el resto del profesorado del departamento de matem¨¢ticas la utilice en los diferentes grupos del centro.

A continuaci¨®n, os invitamos a escuchar la siguiente grabaci¨®n con las valoraciones expresadas, a este respecto, por dos profesionales del IESO ¡®V¨ªa Dalmacia¡¯: Sandra Anes Gallego, profesora de matem¨¢ticas y ?lvaro Pablos Lamas, profesor de inform¨¢tica.

©¤ Jos¨¦ Pedro Mart¨ªn: ¡°Mi objetivo en esta unidad no es que los estudiantes guarden en su memoria el Teorema de Pit¨¢goras y las f¨®rmulas de ¨¢reas y per¨ªmetros de las figuras planas, sino que sepan aplicarlas el d¨ªa que las tengan delante de sus ojos. ?se era el objetivo final.

La f¨®rmula del ¨¢rea de cualquier figura plana la tienen en cinco segundos si la buscan en el m¨®vil, lo verdaderamente importante es que distingan esa figura plana y apliquen lo aprendido. En eso fundamento mi esfuerzo como docente y creo que, con los contenidos contextualizados y a la vista de los resultados alcanzados, se consigue.¡±

Cualquier innovaci¨®n necesita contar para su puesta en pr¨¢ctica con el conocimiento, no solo de la materia o del ¨¢mbito curricular determinado sino, adem¨¢s, de las singularidades que supone el proceso de apropiaci¨®n organizativa, cultural y de aprendizaje adulto docente y de las familias. La generalizaci¨®n de toda propuesta de cambio se encuentra en la evitaci¨®n del fracaso y en la vivencia de la satisfacci¨®n por la mejora conseguida.

Para lograrlo es necesario anticipar y contar con referencias acerca de la complejidad de cualquier innovaci¨®n. Es preciso acercarse a las rutinas profesionales de los docentes, a sus experiencias, actitudes ante el cambio... Sabemos que su viabilidad no es una cuesti¨®n de buena o mala voluntad es, sobre todo, una trama de preparaci¨®n ante el cambio, de capacidad de asimilaci¨®n y experiencia de ¨¦xito.

Hay que buscar el equilibrio entre la zona de desarrollo pr¨®ximo organizativo, cultural, cognitivo, emocional y social del docente y la complejidad del cambio a introducir.

Experiencias como la presente son muy ¨²tiles por las referencias que facilitan, sobre c¨®mo proceder en la promoci¨®n de cambios en las organizaciones educativas.

(*) Versi¨®n para profesionales: ResearchGate (Descargar en PDF).

(**) Jos¨¦ Pedro Mart¨ªn Lorenzo es profesor de matem¨¢ticas en el IESO ¡®V¨ªa Dalmacia¡¯ de Torrejoncillo (C¨¢ceres). Ha desempe?ado cargos directivos en el centro desde el curso 2009/2010 como secretario, y en el curso 2017/2018 pas¨® a desempe?ar el puesto de director, cargo que actualmente ostenta. Hasta el curso 2017/2018 fue uno de los promotores y coordinador de la Plataforma de Radios Escolares de Extremadura¨C RadioEdu que ahora se ha integrado en el Proyecto INNOVATED de la Consejer¨ªa de Educaci¨®n y Empleo de la Junta de Extremadura. En marzo de 2019 fue nombrado presidente de la Sociedad Extreme?a de Educaci¨®n Matem¨¢tica ¡°Ventura Reyes Pr¨®sper¡±.

(**) Gracias al profesorado y al resto de componentes de la comunidad educativa del IESO ¡®V¨ªa Dalmacia¡¯por impulsar, acoger y prestar apoyo a este tipo de iniciativas educativas innovadoras.

(***) Agradecemos la colaboraci¨®n del profesor e ilustrador Joseba Garc¨ªa Plazuelo en la composici¨®n del presente post.