Desaf¨ªo criptogr¨¢fico: c¨®mo acertar la contrase?a en un teclado manipulado

La empresa EscapaEsp, que dise?a retos para salas de escape, ha recibido un encargo de un canal de YouTube: un concurso en el que equipos de 10 personas se enfrenten a varias pruebas. La encargada del canal, una famosa youtuber, quiere ofrecer un premio suculento para los ganadores, pero para ello quiere estar completamente segura de que, a lo sumo, solo van a ganar tres de cada diez equipos. Adem¨¢s, le gustar¨ªa dar la impresi¨®n de que el juego es dif¨ªcil de ganar.

Julia y Juan, encargados de dise?ar los retos en EscapaEsp, intercambian ideas hasta alcanzar una propuesta. Cada equipo deber¨¢ enfrentarse a diferentes pruebas para ir encontrando los diez caracteres de una contrase?a. Al final de las pruebas, todos los equipos pasar¨¢n a una fase final en la que los miembros del grupo competidor entrar¨¢n de uno en uno en una sala en la que solo hay un teclado y una pantalla. Cada uno escribir¨¢ un car¨¢cter de la contrase?a. Para ganar, han de conseguir que la pantalla del ordenador muestre los diez caracteres de la contrase?a en el orden correcto.

La prueba, desde luego, no ser¨¢ sencilla; ni siquiera para los equipos que conocen la contrase?a al completo: el teclado est¨¢ manipulado, de forma que lo escrito en el teclado no se corresponde con lo mostrado en pantalla. En concreto, Julia y Juan han propuesto las siguientes reglas:

1) La contrase?a no tiene ning¨²n car¨¢cter repetido, y los caracteres solo pueden estar entre los 40 siguientes: las 27 letras del abecedario espa?ol (con la ¡°?¡±), el punto, el guion, la coma y los diez d¨ªgitos (0- 9).

2) El teclado tiene ¨²nicamente los 40 caracteres anteriores. Adem¨¢s, se han manipulado los cables aleatoriamente, de forma que, al pulsar una tecla, lo m¨¢s probable es que no aparezca en la pantalla el car¨¢cter pulsado. Es decir, al pulsar la tecla ¡°m¡± quiz¨¢s se muestre el car¨¢cter ¡°8¡å. No obstante, esta manipulaci¨®n se mantiene igual a lo largo de todo el juego (si la tecla ¡°m¡± hace aparecer ¡°8¡å, lo har¨¢ para todos los jugadores del mismo equipo). Adem¨¢s, no hay dos teclas que hagan aparecer en pantalla el mismo car¨¢cter.

3) ¡¤ Los jugadores que han entrado en la sala del teclado deber¨¢n salir por una puerta diferente de la entrada, y no podr¨¢n comunicarse con los jugadores que a¨²n esperan su turno. Del mismo modo, aunque se pueda mostrar a los espectadores lo que ocurre en la sala del teclado, los jugadores que no han entrado no deben saber nada. Es decir, cada jugador del equipo que entre en la sala del teclado debe tener la misma informaci¨®n que el primero que se enfrent¨® al teclado.

4) ¡¤ Los caracteres de la contrase?a se deben introducir en orden: el primer jugador que entre en la sala deber¨¢ introducir el primer car¨¢cter, el segundo introducir¨¢ el segundo car¨¢cter y as¨ª con todos.

5) ¡¤ Cuando un jugador se enfrenta al teclado, podr¨¢ probar hasta un m¨¢ximo de 20 teclas distintas para hacer aparecer su car¨¢cter. En el momento en el que el car¨¢cter correcto aparezca, una luz verde se encender¨¢ y podr¨¢ pasar el siguiente jugador, independientemente de si el jugador conoc¨ªa o no el car¨¢cter correcto antes de entrar. Si tras la pulsaci¨®n 20 alg¨²n jugador no logra obtener la luz verde, todo el equipo habr¨¢ perdido.

6) ¡¤ Los diez jugadores pueden dise?ar cooperativamente una estrategia antes de enfrentarse al juego.

La youtuber hace un c¨¢lculo r¨¢pido y determina que la probabilidad de ¨¦xito de cada miembro del equipo es ? . Como todos tienen la misma informaci¨®n al entrar, al ser 10 jugadores en el equipo, su probabilidad de ¨¦xito es de ? * ? * ¡­ * ? (10 veces) , aproximadamente 0,001. Esto le choca por dos motivos. En primer lugar, parece que la probabilidad de ganar es independiente de si la contrase?a es conocida o no, ya que el ordenador autom¨¢ticamente valida la clave cuando se introduce el car¨¢cter correcto. Y eso le parece injusto: el equipo que conozca toda la contrase?a debe tener una ventaja. En segundo lugar, esta probabilidad le parece demasiado escasa. Que haya equipos que ganen hace que m¨¢s gente se interese por el programa. Y tambi¨¦n que m¨¢s equipos quieran participar.

Sin embargo, Julia y Juan explican que existe una estrategia que garantiza que la probabilidad de ¨¦xito del equipo, si conocen la contrase?a al completo, es de 0,32. Si ¨²nicamente conocen algunas partes de la contrase?a, la probabilidad de ganar se reduce: por ejemplo, si conocen 7 caracteres, no han podido dar con una estrategia que ofrezca un ¨¦xito con probabilidad superior a 0,04.

?Puede el lector encontrar cu¨¢l es esta estrategia que deber¨ªan seguir los concursantes para ganar aproximadamente tres de cada diez veces si conocen toda la contrase?a? ?Por qu¨¦ es tan importante conocer la contrase?a para maximizar las opciones de ganar?

Los desaf¨ªos criptogr¨¢ficos se publicar¨¢n cada 15 d¨ªas. Los lectores pueden dejar sus soluciones y debatir sobre el problema en los comentarios de esta p¨¢gina, por lo que se recomienda a quien quiera resolverlo por s¨ª mismo no leerlos hasta haber descifrado el enigma. Tambi¨¦n pueden enviar sus respuestas al correo desafioscriptograficos@gmail.com. En cada nuevo desaf¨ªo publicaremos la soluci¨®n del anterior, acompa?ada de un comentario con algunas ideas originales o inspiradoras que hayamos recibido.

Diego Castej¨®n Molina y David Balb¨¢s Guti¨¦rrez son investigadores predoctorales en el Instituto IMDEA Software de Madrid. Su trabajo se centra en el dise?o y an¨¢lisis de protocolos criptogr¨¢ficos y aplicaciones.

SOLUCI?N AL DESAF?O ANTERIOR

Esta quincena hemos recibido multitud de respuestas, ?gracias a todos por sus comentarios!

Para calcular el orden correcto orden utilizamos el mecanismo enunciado, que, aunque de manera simplificada, es el que sigue la criptomoneda Bitcoin, propuesta en 2008 bajo el pseud¨®nimo de Satoshi Nakamoto. Principalmente, nos fijamos en el valor BA, que es un puntero al bloque anterior. En concreto, BA indica el resto de calcular la divisi¨®n entera del bloque anterior por 541. As¨ª, por ejemplo, el segundo bloque lo encontramos al calcular la divisi¨®n entera de 53244 entre 541. El resto, 226, nos indica cu¨¢l es el segundo bloque (aquel que tiene 226 como BA). Por el mismo procedimiento podemos encontrar el tercer bloque. Al calcular la divisi¨®n entera de 22623138 por 541, el resto, 141, nos anuncia el tercer bloque. Para calcular el cuarto bloque primero se tendr¨¢ que calcular el valor de B del tercer bloque. Recordad que se trata de encontrar un valor tal que 141112XXXXX (donde las X son d¨ªgitos diferentes, y la longitud no es fija) tal que al calcular la divisi¨®n entera de 141112XXXX^3 y 541, el resto acabe con dos ceros. Se trata de ir probando valores (una sugerencia es programarlo, usando un comando del estilo Table[H[141112*10 + k], {k, 0, 9}] ¨Dsi suponemos que encontraremos la soluci¨®n a?adiendo un solo d¨ªgito¨D o Table[H[141112*10^2 + k], {k, 0, 99}] ¨Dpara probar con dos d¨ªgitos¨D etc,). Con esa t¨¦cnica, se obtiene que 39 lo cumple. As¨ª, podemos calcular el valor BA del cuarto bloque, que ser¨¢ el resto de calcular la divisi¨®n entera entre 14111239 y 541. El resultado, 336, nos anuncia el cuarto bloque. El restante, por lo tanto, ser¨¢ el ¨²ltimo de los bloques.

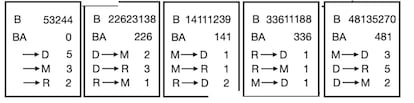
Nota: Para los que sepan aritm¨¦tica modular, las operaciones que estamos haciendo al calcular las divisiones enteras y quedarnos con el resto, es el c¨¢lculo del dividendo m¨®dulo el divisor.

Una vez tenemos los bloques ordenados, podemos mirar qu¨¦ dinero tienen los hermanos. Recogemos el resultado en la siguiente tabla, donde la ¨²ltima columna es el resultado final.

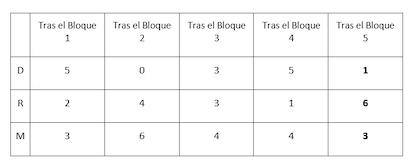
Aunque, como varios hab¨¦is se?alado, si no hay bloques inv¨¢lidos las transacciones propuestas en el reto ¡°conmutar¨ªan¡±, y mirando el saldo final la soluci¨®n es la misma, si los bloques no se ordenan bien no podemos dar la soluci¨®n por correcta. La raz¨®n (muy importante en el mundo real) es que ordenando los bloques de cualquier manera a menudo aparecen transacciones intermedias inv¨¢lidas: es decir, alguien tiene que transferir m¨¢s de lo que tiene en ese momento.

Nota: Aparte de la simplificaci¨®n en los contenidos, hay que tener en cuenta la importancia de los formatos, que aqu¨ª se han simplificado tambi¨¦n para focalizar la explicaci¨®n en el mecanismo. Puede que a algunos les sea familiar la noci¨®n de funci¨®n resumen (o hash) y que se utilizan en numerosos escenarios de la vida cotidiana, desde las firmas digitales hasta cuando guardamos una contrase?a. Lo que hace un minero al minar, no es calcular el cubo de ciertos valores, sino que calcular¨¢ convenientemente una funci¨®n hash, en particular una de las m¨¢s utilizadas en la actualidad, la funci¨®n SHA-256. Por simplicidad, tambi¨¦n hemos omitido la (muy importante) parte en la que se autentican los mensajes, las firmas digitales son de gran ayuda en este contexto.

PS: Tal y como prometimos la semana pasada, incluimos tambi¨¦n la soluci¨®n al desaf¨ªo criptogr¨¢fico-musical que nos envi¨® nuestro lector Salva Fuster.

- ?Qu¨¦ melod¨ªa act¨²a como clave (hay que tener en cuenta que en la clave, las F realmente son F#)?

La primera suite de Bach para violonchelo BWV 1007.

- ?Cu¨¢l es la palabra oculta?

ENHORABUENA

- ?Cu¨¢l es el sistema que permite cifrar/descifrar el mensaje?

Para cifrar un mensaje, ¨²nicamente lo convertimos en binario, como en el desaf¨ªo Un mensaje en clave napolitana oculto entre unos y ceros y, a partir de una determinada melod¨ªa escogida previamente (que act¨²a como clave), creamos una nueva de tal manera que sea disonante con la melod¨ªa clave para obtener un 0, y consonante para obtener un 1. En particular, se ha elegido una alternancia de notas musicales inferiores y superiores a las de la clave para las disonancias, y una cuarta justa (o quinta justa) para las consonancias, aunque se hubiera podido complicar un poco m¨¢s eligiendo aleatoriamente otros tipos de disonancias y consonancias.

Para descifrarlo, ¨²nicamente cabr¨ªa hacer lo mismo, pero en sentido inverso, es decir, identificar las disonancias y consonancias de la melod¨ªa recibida respecto a la melod¨ªa que act¨²a como clave para convertirlas en las correspondientes cifras 0 y 1, y, posteriormente, transformar el c¨®digo binario obtenido en el mensaje en claro.

Otro infatigable lector, Xuacu ?lvarez, ha dado con la soluci¨®n correcta (ENHORABUENA, nunca mejor dicho, tambi¨¦n para ¨¦l por acertar).

Fe de errores: En una primera versi¨®n de este art¨ªculo inclu¨ªamos las dudas sobre la soluci¨®n que nos hab¨ªa transmitido Xuacu ?lvarez. Pero en un segundo correo (al que incluso contestamos, ?ay qu¨¦ cabeza la nuestra!), nos confirmaba que sus dudas hab¨ªan quedado aclaradas. Nuestras disculpas y, de nuevo, nuestro agradecimiento a ¨¦l y a Salva.

Puedes seguir a EL PA?S TECNOLOG?A en Facebook y Twitter o apuntarte aqu¨ª para recibir nuestra newsletter semanal.