Desaf¨ªo criptogr¨¢fico: ?Que le corten la cabeza! O no¡­

¨C?Que le corten la cabeza! ¨Cexclam¨® enfurecida la Reina de Corazones.

¨CBueno, bueno, querida, primero tendremos emitir cada uno nuestro voto, ?no es as¨ª? ¨Cdijo con tranquilidad el Rey de Corazones.

¨C?No! ?Estoy harta de este sistema de votaciones que acordamos! Decidimos que para cortar una cabeza es necesario que los dos estemos a favor, ?sabes ni?a? ¨Cdijo la Reina dirigi¨¦ndose a Alicia, que era la ¨²nica que parec¨ªa no estar al tanto.

¨C?Y cu¨¢l es el problema, Su Majestad? ?Desea decidir usted sola? ¨Crespondi¨® Alicia educadamente.

¨CNo ni?a, ese no es el problema en absoluto, estoy de acuerdo en que lo hagamos conjuntamente. Pero el desenlace habitual es que yo voto ¡°cortar¡± y el Rey ¡°vota perdonar¡±, el acusado se salva y, para colmo, todo el mundo piensa que soy una persona horrible.

¨C?Y no lo arreglar¨ªan votando en secreto? Cada uno de ustedes podr¨ªa darle el voto en un sobre cerrado a alguien de confianza, por ejemplo, al Conejo Blanco. Cuando tuviera los dos votos en su poder, anunciar¨ªa si el acusado ha sido perdonado o no, sin revelar nada m¨¢s sobre la votaci¨®n.

¨CPero, ?qu¨¦ ingenua eres! Alguien de confianza, dices. Ya lo hemos intentado y siempre se acaba sabiendo el voto de cada uno. No me f¨ªo absolutamente de nadie.

¨CMajestad, he estado d¨¢ndole vueltas al asunto y creo que podr¨ªa haber una soluci¨®n ¨C intervino el Sombrerero¨C. Podr¨ªamos intentar dise?ar un nuevo Protocolo Real en el que solo intervinieran el Rey y usted. Tras llevarlo a cabo, se sabr¨ªa si el acusado se salva o no. Pero usted obtendr¨ªa ciertas garant¨ªas de privacidad. Si rodara la cabeza, estar¨ªa claro lo que ha votado cada uno, nada que ocultar ah¨ª. Pero si el acusado se salvase y el Rey hubiera votado ¡°perdonar¡±, lo que usted ha votado quedar¨ªa en secreto para todo el mundo, incluido el propio Rey. As¨ª, su reputaci¨®n se mantendr¨ªa a salvo. Por supuesto, el Rey obtendr¨ªa las mismas garant¨ªas.

¨C?Ya est¨¢s con tus est¨²pidas ideas! Es evidente que eso es imposible. ?Qu¨¦ le corten la¡­! En fin, da igual, seguro que el Rey te va a perdonar.

¨CCon todos los respetos, Su Majestad, quiz¨¢ no sea imposible ¨Cdijo t¨ªmidamente Alicia¨C. Una vez, en mi tierra, estuve en una conferencia en un lugar llamado Laboratorio Idea. El profesor que la imparti¨®, Miguel, habl¨® de un problema muy parecido al que ha planteado el Sombrerero, de hecho, yo dir¨ªa que es exactamente el mismo. Bueno, no hab¨ªa que cortarle la cabeza a nadie, pero por lo dem¨¢s era el mismo. Y adem¨¢s explic¨® una forma de resolverlo. Os podr¨ªa contar lo que recuerdo, pero tengo algunas lagunas. Hacen falta seis cartas con dorsos id¨¦nticos, esto os agradar¨¢. De las seis cartas, tres han de ser iguales, por ejemplo, tres ases de corazones y las otras tres diferentes de las primeras pero iguales entre s¨ª, por ejemplo, tres ases de picas. Usted tendr¨ªa dos cartas para votar, una roja y una negra; y lo mismo para el Rey. Las dos cartas restantes se colocan en una mesa con seis espacios. Os har¨¦ un dibujo.

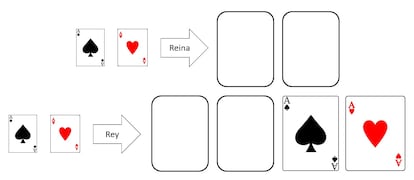
¨CEstas dos cartas se pondr¨ªan ahora bocabajo. Para votar, cada uno de ustedes pondr¨ªa sus dos cartas, tambi¨¦n bocabajo, en los espacios que les estoy indicando. Si la carta roja est¨¢ a la izquierda, el voto es ¡°Cortar¡±, mientras que, si est¨¢ a la derecha, el voto es ¡°Perdonar¡±. Aqu¨ª es donde mis recuerdos no son ya precisos. Hab¨ªa que dividir esas seis cartas, de alguna manera, en dos grupos de tres cartas, grupo 1 y grupo 2, e introducir cada grupo ordenadamente en un sobre cerrado. A continuaci¨®n, los sobres se mezclaban para que no pudiera saberse cu¨¢l conten¨ªa las cartas de cada grupo. Se abr¨ªa por tanto un sobre y se colocaban las cartas (sin alterar el orden) asumiendo que eran las del grupo 1, para hacer despu¨¦s lo propio con el grupo 2 y el segundo sobre. Finalmente mostrando solo cuatro de las seis cartas pod¨ªa verse el resultado. Siento no recordar todos los detalles, Majestad.

¨CInteresante, s¨ª, muy interesante. ?Sombrerero! ?Ser¨ªas capaz de completar el nuevo Protocolo Real a partir de estas ideas?

La soluci¨®n de este d¨¦cimo y ¨²ltimo desaf¨ªo criptogr¨¢fico se publicar¨¢ dentro de 15 d¨ªas. Los lectores pueden dejar sus soluciones y debatir sobre el problema en los comentarios de esta p¨¢gina, por lo que se recomienda a quien quiera resolverlo por s¨ª mismo no leerlos hasta haber descifrado el enigma. Tambi¨¦n pueden enviar sus respuestas al correo desafioscriptograficos@gmail.com.

Angel L. P¨¦rez del Pozo es profesor de Matem¨¢tica Aplicada e investigador en Criptograf¨ªa en la U. Rey Juan Carlos.

SOLUCI?N AL DESAF?O ANTERIOR

El desaf¨ªo de esta semana se ha resistido un poco m¨¢s (incluso a nuestros lectores m¨¢s habituales y aventajados). Intuitivamente, puede parecer que la youtuber est¨¢ en lo cierto cuando afirma que la probabilidad de ¨¦xito de un miembro del equipo no depende que ¨¦ste conozca la clave o no. Y de hecho, est¨¢ completamente en lo cierto al pensar que, como todos los miembros del equipo entran a la sala con la misma informaci¨®n, no pueden influirse unos a otros para amplificar su ventaja.

A pesar de todo, s¨ª que existe una estrategia que aumenta la probabilidad de ¨¦xito del equipo que conoce la contrase?a. La observaci¨®n clave es la siguiente. Como no hay dos teclas que escriban el mismo car¨¢cter en pantalla, cada car¨¢cter est¨¢ asociado de forma ¨²nica a cada tecla. Si empezamos pulsando la tecla ¡°1¡å y aparece el car¨¢cter ¡°x¡±, podemos pulsar la tecla ¡°x¡±, que mostrar¨¢ por ejemplo el ¡°8¡å. La tecla ¡°8¡å mostrar¨¢ el ¡°k¡±, la ¡°k¡± el ¡°q¡±, etc. Esto define una secuencia que podemos describir de la siguiente manera: (1-x-8-k-q-¡­). Dicho de otro modo, las teclas definen una permutaci¨®n, que adem¨¢s es aleatoria, del conjunto de 40 caracteres posibles.

Cuando definimos una permutaci¨®n al azar, es improbable que podamos escribirla por completo en una sola secuencia. Por ejemplo, si resulta que tecla ¡°q¡± muestra el car¨¢cter ¡°1¡å, se forma la secuencia (1-x-8-k-q-1). Si pulsamos la tecla ¡°1¡å, volveremos a obtener una ¡°x¡± y as¨ª sucesivamente, quedando atrapados en un ciclo. Para continuar, debemos elegir una tecla distinta de las anteriores, como por ejemplo la tecla ¡°2¡å, que dar¨¢ lugar a otra secuencia (o ciclo) diferente. En general, necesitaremos varios ciclos de este tipo para describir la permutaci¨®n al completo.

Para ilustrar la estrategia a seguir, centr¨¦monos en el primer miembro del equipo, cuya tarea es conseguir que aparezca su car¨¢cter en la pantalla, por ejemplo, la letra ¡°q¡±. Debe comenzar pulsando la tecla ¡°q¡± correspondiente a su car¨¢cter, y avanzar en la secuencia anterior hasta encontrar la tecla que muestre la ¡°q¡± en pantalla. Por ejemplo, (q-1-x-8-k-q), con lo que habr¨¢ encontrado la tecla que muestra la ¡°q¡± (es decir, la tecla ¡°x¡±) en cinco pasos. Si todos los miembros del equipo siguen esta estrategia, tendr¨¢n garantizado ganar si todos los ciclos de la permutaci¨®n tienen una longitud menor que 20, que es el n¨²mero de teclas que pueden pulsar. Si existe alg¨²n ciclo de longitud mayor que 20, lo m¨¢s probable es que alg¨²n miembro del equipo fracase.

La probabilidad de que, dada una permutaci¨®n al azar de 40 elementos, todos los ciclos sean de longitud menor que 20 es de un 32%. El problema se inspira en el conocido como ¡°problema de los 100 prisioneros¡±, propuesto por Peter Bro Miltersen en 2003. Nuestro lector, Anghlar, se ha dado cuenta r¨¢pidamente. Para los m¨¢s curiosos, un desarrollo matem¨¢tico del problema original puede encontrarse en esta p¨¢gina.

Es probable que, en este punto, el lector se pregunte: ?y c¨®mo puedo estar seguro de que voy a encontrar mi car¨¢cter en la secuencia? La clave est¨¢ en que, al empezar por la tecla correspondiente a tu car¨¢cter, te aseguras de encontrarlo al final del ciclo, en tantos pasos como la longitud del mismo. Invitamos al lector a dibujar las posibles secuencias, por ejemplo en permutaciones de n¨²meros del 1 al 10, para ver este fen¨®meno con claridad. De hecho, esto es lo que proporciona una ventaja a los conocedores de la clave; un jugador que busque un car¨¢cter que no conoce no podr¨¢ empezar por ¨¦l, y por tanto no tendr¨¢ garantizado ¡°caer¡± en el ciclo que lo contiene. La probabilidad de ¨¦xito en este caso se reduce a un 50% por jugador, como planteaba la youtuber.

Con este reto, presentamos un problema en el que aparentemente la probabilidad de ¨¦xito es pr¨¢cticamente nula, pero para el que existe una estrategia que permite obtener una victoria casi una de cada tres veces. Esto ilustra la importancia de realizar pruebas (matem¨¢ticas) de seguridad rigurosas para los protocolos criptogr¨¢ficos, pues si se dise?a un protocolo que carezca de tal an¨¢lisis, es posible que se den ataques devastadores.

Como curiosidad final, estrategias similares de b¨²squeda de ciclos dan lugar a algoritmos con aplicaciones pr¨¢cticas importantes, como por ejemplo la factorizaci¨®n de enteros.

Puedes seguir a EL PA?S TECNOLOG?A en Facebook y Twitter o apuntarte aqu¨ª para recibir nuestra newsletter semanal.