17 maneras de decorar su pared: los grupos de papel pintado

Desde los or¨ªgenes de la humanidad las matem¨¢ticas han jugado un papel importante en el desarrollo de las artes. En concreto, una de las relaciones m¨¢s interesantes entre estas dos disciplinas se encuentra en el estudio de los patrones. A lo largo de la historia, las decoraciones con elementos repetidos se han utilizado tanto en tumbas egipcias, como en frisos griegos, jarrones chinos, en los populares grabados del artista M. C. Escher o¡­ en los papeles pintados que podemos encontrar en cualquier hogar.

Este tipo de decoraciones motiv¨® el avance de toda un ¨¢rea de las matem¨¢ticas: la teor¨ªa de grupos. Esta se emple¨® para clasificar los patrones existentes. Muchos matem¨¢ticos importantes se lanzaron a la tarea que no result¨® ser tan simple como parec¨ªa.

A priori podr¨ªa haber infinitos patrones diferentes. Sin embargo, parecen agruparse en categor¨ªas. Usualmente, cualquier tipo de patr¨®n tiene 'regularidades' o maneras de repetirse, esto es, si lo movi¨¦ramos de cierto modo, el dibujo se mantendr¨ªa igual. Este tipo de movimientos son las simetr¨ªas.

Los ingredientes b¨¢sicos para construir simetr¨ªas son las traslaciones, las rotaciones y las reflexiones. Las traslaciones desplazan el patr¨®n en una direcci¨®n determinada, hasta que vuelve a encajar con el original. Los giros mueven todo el patr¨®n un ¨¢ngulo determinado, alrededor de un punto. Las reflexiones son un movimiento especular sobre una l¨ªnea, de manera que lo que queda a un lado de ella es un reflejo de lo que queda al otro.

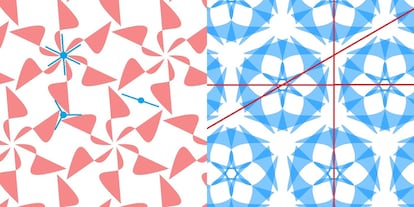
Las simetr¨ªas de los patrones se configuran con estos movimientos. Los giros y las reflexiones son las primeras. Lo siguiente son dobles traslaciones, es decir, desplazar el patr¨®n en dos direcciones distintas de manera que obtengamos lo mismo de nuevo. Finalmente, est¨¢ la combinaci¨®n de reflexi¨®n y traslaci¨®n, por la cual movemos el patr¨®n en una direcci¨®n y luego le aplicamos una reflexi¨®n. Esta es la simetr¨ªa m¨¢s dif¨ªcil de visualizar, aunque es menos frecuente.

Partiendo de estas cuatro simetr¨ªas para crear una decoraci¨®n, los matem¨¢ticos se preguntaron cu¨¢ntas combinaciones eran posibles. En 1891 el matem¨¢tico ruso Yevgraf Fi¨®dorov fue el primero en demostrar que, aunque hay infinitas im¨¢genes con las cuales formar patrones, ?en realidad solo hay 17 combinaciones diferentes de simetr¨ªas! Estas 17 recetas que permiten clasificar patrones son los llamados grupos cristalogr¨¢ficos planos, tambi¨¦n conocidos con el nombre m¨¢s inofensivo de grupos de papel pintado.

Aunque las herramientas que se usan para demostrar que, efectivamente, solo existen 17 grupos son bastante modernas, es sorprendente constatar que este resultado se conoc¨ªa (al menos intuitivamente) en la antig¨¹edad. Efectivamente, en un edificio tan emblem¨¢tico como la Alhambra, podemos hallar los 17 grupos representados como decoraciones de paredes y suelos. En 1922 Escher visit¨® este monumento para inspirarse en sus grabados geom¨¦tricos.

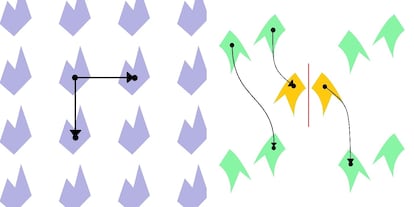
El mismo problema, en tres dimensiones o m¨¢s, da lugar a cat¨¢logos m¨¢s amplios ya que, aparentemente, podemos encontrar muchas m¨¢s combinaciones de simetr¨ªas. El primero en plantearse esta cuesti¨®n fue David Hilbert en 1900, y corresponde a uno de sus famosos problemas del milenio: ?hay siempre un n¨²mero finito de grupos cristalogr¨¢ficos en cualquier dimensi¨®n? Diez a?os despu¨¦s, el matem¨¢tico Ludwig Bieberbach contest¨® afirmativamente a esta cuesti¨®n, aunque no pudo especificar cu¨¢ntos grupos se obtienen exactamente en cada dimensi¨®n. Para entender la dificultad del problema, hay que tener en cuenta que en tres dimensiones hay 230 grupos diferentes, 4783 en dimensi¨®n cuatro y 222.018 en dimensi¨®n 5. A¨²n se desconocen cuantos hay para dimensi¨®n mayor que 6.

Estos grupos (y en particular los de tres dimensiones) tienen aplicaciones m¨¢s all¨¢ de lo puramente est¨¦tico. Son ampliamente utilizados en cristalograf¨ªa qu¨ªmica y f¨ªsica, geolog¨ªa e incluso arquitectura.

Julio Aroca es investigador predoctoral en la Universidad Aut¨®noma de Madrid y miembro del ICMAT.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter