El premio Abel reconoce a dos pioneros de la interacci¨®n entre probabilidad y ¨¢lgebra

Los matem¨¢ticos Hillel Furstenberg y Gregory Margulis han sido los ganadores del premio Abel 2020. Se les concede ¡°por ser pioneros en el uso de m¨¦todos probabil¨ªsticos y din¨¢micos en las ¨¢reas de teor¨ªa de grupos, teor¨ªa de n¨²meros y combinatoria.¡± Lo cierto es que Furstenberg y Margulis nunca han trabajado juntos; es m¨¢s, ni han vivido en el mismo continente simult¨¢neamente.

Margulis (1946, Mosc¨²) trabaj¨® toda su juventud bastante aislado del resto de la comunidad matem¨¢tica, v¨ªctima de la discriminaci¨®n que ejerc¨ªa la Uni¨®n Sovi¨¦tica sobre los jud¨ªos en esos tiempos. La situaci¨®n lleg¨® al extremo cuando, en 1978, la Uni¨®n Matem¨¢tica Internacional le concedi¨® la medalla Fields y el Gobierno no le concedi¨® un visado para ir a Helsinki y aceptarla en persona.

Furstenberg tambi¨¦n es jud¨ªo, de hecho es el primer israel¨ª que recibe el premio Abel. Naci¨® en Berl¨ªn en 1935, en medio de la ocupaci¨®n nazi, pero con solo tres a?os, despu¨¦s de la Noche de los Cristales Rotos, huy¨® con su familia a los Estados Unidos, donde desarroll¨® los primeros a?os de su carrera.

Furstenberg y Margulis, de manera independiente, utilizaron ideas y t¨¦cnicas probabil¨ªsticas similares para estudiar el mismo tipo de objetos matem¨¢ticos. No es la primera vez, ni ser¨¢ la ¨²ltima, que varios investigadores descubren el poder de las mismas ideas de manera paralela y en el mismo periodo de tiempo. Quiz¨¢s el ejemplo m¨¢s famoso es el del c¨¢lculo diferencial, desarrollado simult¨¢neamente en Inglaterra por Isaac Newton y en Alemania por Gottfried Leibniz. A diferencia de aquella agria disputa, es bonito y justo que el premio Abel de este a?o haga un reconocimiento compartido a dos personas que contribuyeron a desarrollar la matem¨¢tica con el mismo tipo de ideas revolucionarias.

Las t¨¦cnicas que Margulis introdujo en su demostraci¨®n siguen siendo muy importantes hoy en d¨ªa. Y, sorprendentemente, permitieron descubrir nuevas e importantes propiedades de los grupos de matrices

Uno de los teoremas m¨¢s famosos de Furstenberg trata sobre los caminos aleatorios en grupos infinitos de matrices. Para entender la noci¨®n de camino aleatorio, imaginemos que tenemos un dado (equilibrado) de cuatro caras y un papel cuadriculado (de dimensi¨®n 2), infinito. Cada una de las caras del dado representa un movimiento: hacia arriba, abajo, izquierda o derecha. Empezamos en un cuadrado de la libreta, y seguimos el movimiento que van marcando los sucesivos lanzamientos del dado. El resultado es un camino aleatorio.

El matem¨¢tico George Polya ya sab¨ªa, en los a?os 1930, que un camino as¨ª volver¨ªa al punto inicial un n¨²mero infinito de veces, con un 100% de probabilidades. Sin duda, es posible (aunque improbable) que los lanzamientos del dado dicten que la marcha vaya a la derecha para siempre. Esto no contradice la conclusi¨®n de Polya, pues si consideramos todos los caminos, es decir todas las posibilidades de movimientos con el mismo punto inicial, la probabilidad de que uno regrese al punto inicial (un n¨²mero finito de veces) es 0. Polya tambi¨¦n sab¨ªa que, sin embargo, si repetimos el mismo experimento en una cuadr¨ªcula de dimensi¨®n 3, la probabilidad de volver al punto inicial un n¨²mero infinito de veces es 0. As¨ª, el camino aleatorio es capaz de detectar la diferencia entre dimensi¨®n 2 y 3.

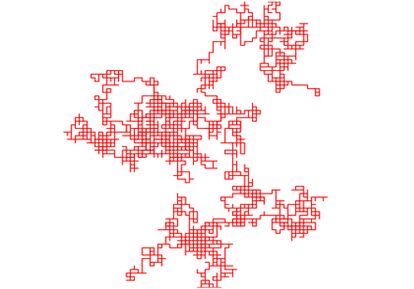
Furstenberg consider¨® estos caminos aleatorios no en una cuadr¨ªcula, sino en espacios de matrices. La idea es parecida: tomamos un conjunto finito de matrices, por ejemplo, seis matrices A,B,C,D,E, F; y un dado de seis caras, en cuyas caras est¨¢n escritas la letras A,B,C,D,E,F. As¨ª vamos lanzando el dado y multiplicando matrices de la siguiente manera: por cada lanzamiento multiplicamos la matriz que dicta el dado (a la izquierda) del producto acumulado de las matrices anteriores. Aqu¨ª es muy importante el orden, ya que la multiplicaci¨®n de matrices no es conmutativa. Como el producto de matrices es de nuevo un matriz, de esta forma, los lanzamientos dan una secuencia de matrices, lo que configura un camino aleatorio dentro del espacio de matrices. Furstenberg estudi¨® su avance y comprob¨® que, a diferencia de lo que suced¨ªa en la cuadr¨ªcula, los caminos aleatorios siempre se alejan y llegan a una frontera asociada a ese conjunto finito de matrices: la frontera Furstenberg-Poisson.

Por su parte, uno de los teoremas m¨¢s conocidos de Margulis describe la s¨²per-rigidez de ret¨ªculos de matrices. Es un resultado de la zoolog¨ªa de los llamados grupos de Lie, que demuestra que cualquier grupo est¨¢ esencialmente determinado por su esqueleto. Las t¨¦cnicas que Margulis introdujo en su demostraci¨®n siguen siendo muy importantes hoy en d¨ªa. Y, sorprendentemente, permitieron descubrir nuevas e importantes propiedades de los grupos de matrices.

No es la primera vez, ni ser¨¢ la ¨²ltima, que varios investigadores descubren el poder de las mismas ideas de manera paralela y en el mismo periodo de tiempo

Una propiedad de grupos que Margulis utiliz¨® mucho en sus trabajos sobre grupos es la llamada propiedad (T). En 1973, la emple¨® para ofrecer una construcci¨®n expl¨ªcita de grafos expanders. Un grafo expander es una secuencia de grafos finitos que son uniformemente eficientes y robustos. Imaginemos que una empresa quiere conectar 100 ordenadores entre s¨ª. Lo ideal ser¨ªa que cada ordenador est¨¦ solamente conectado con otros pocos terminales; pero que adem¨¢s sea muy dif¨ªcil desconectar todo el sistema, es decir, que no haya dos partes grandes separadas por pocas conexiones. Si lo conseguimos, el resultado ser¨ªa un grafo eficiente (es la primera propiedad indicada) y robusto (la segunda).

El matem¨¢tico George Polya ya sab¨ªa, en los a?os 1930, que un camino as¨ª volver¨ªa al punto inicial un n¨²mero infinito de veces, con un 100% de probabilidades

Antes del trabajo de Margulis, se sab¨ªa que si se conectan los v¨¦rtices de un grafo de forma aleatoria el resultado ser¨¢ eficiente y robusto, con una probabilidad que tiende a 1, cuando el n¨²mero de v¨¦rtices crece al infinito. Es decir, la empresa podr¨ªa conectar los ordenadores al azar y comprobar si ha tenido suerte. Pero probar con todas las combinaciones, solo de 100 ordenadores, requiere c¨¢lculos de magnitudes astron¨®micas. La construcci¨®n expl¨ªcita de Margulis te dice exactamente c¨®mo hacerlo.

Tanto las matem¨¢ticas de Furstenberg como las de Margulis utilizan ideas de ¨¢reas diferentes y de formas muy sorprendentes para concluir sus teoremas. Leer sus pruebas es como ver una pel¨ªcula de suspense, con sorpresas y conexiones inesperadas en cada p¨¢gina.

Yago Antol¨ªn es profesor titular de la Universidad Complutense de Madrid y miembro del ICMAT

Talia Fern¨®s es profesora de la Universidad de Carolina del Norte en Greensboro (EE UU).

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n Garc¨ªa-Longoria (ICMAT)

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter.