Matem¨¢ticas para entender y mejorar la democracia

La democracia es un pilar fundamental de muchas sociedades modernas y su correcto funcionamiento depende en gran medida de sistemas de votaci¨®n justos y eficientes. Las matem¨¢ticas permiten dise?ar y comprender estos sistemas desde los trabajos del marqu¨¦s de Condorcet en el siglo XVIII, que dieron lugar a la teor¨ªa de elecci¨®n social. Esta rama de la econom¨ªa matem¨¢tica se centra en entender los procesos de agregaci¨®n de preferencias e informaci¨®n. Estudia, por ejemplo, c¨®mo los distintos sistemas de votaci¨®n pasan de las preferencias de los votantes a los resultados de las elecciones.

Una de las cuestiones relevantes a considerar en la teor¨ªa de elecci¨®n es la propiedad de transitividad, que trata de c¨®mo se relacionan entre s¨ª y se organizan las preferencias de un individuo o colectivo. Por ejemplo, imaginemos que estamos eligiendo entre tres tipos de helados: chocolate, vainilla y fresa (A, B y C). La propiedad de transitividad establece que, si preferimos el helado de chocolate al de vainilla, y preferimos el helado de vainilla al de fresa, entonces tambi¨¦n deber¨ªamos preferir el helado de chocolate al de fresa. Esto es lo que se espera en un conjunto de preferencias racionales.

Violaciones de esta propiedad conducen a resultados ¡°irracionales¡±, como el del Dutch book (y en espa?ol). Imaginemos que tenemos otras preferencias, ahora intransitivas, sobre los helados: A>B, B>C, C>A. Si, de partida, tenemos helado de chocolate, como preferimos el de fresa, estamos dispuestos a intercambiar el nuestro, junto con una peque?a cantidad de dinero ¦Ä (digamos, 1€) por el helado de fresa, por tanto, C>A+¦Ä. A continuaci¨®n, vender¨ªamos C m¨¢s una peque?a cantidad de dinero ¦Ä' para obtener B, ya que preferimos B sobre C. Finalmente, vender¨ªamos B m¨¢s una peque?a cantidad de dinero ¦Ä'¡¯ para obtener A nuevamente, puesto que preferimos A sobre B. Al final del proceso, volver¨ªamos a tener A, pero habr¨ªamos perdido las cantidades de dinero ¦Ä, ¦Ä' y ¦Ä'¡¯ en el proceso.

Las matem¨¢ticas permiten dise?ar sistemas de votaci¨®n justos y eficientes, desde los trabajos de Condorcet en el siglo XVIII, que dieron lugar a la teor¨ªa de elecci¨®n social: los procesos de agregaci¨®n de preferencias de los votantes

Sin embargo, Condorcet mostr¨® que las preferencias a nivel social pueden ser intransitivas, de manera general. Por ejemplo, imaginemos una elecci¨®n con tres candidatos (A, B y C) y tres votantes con preferencias transitivas: el primero, prefiere a A antes que a B y a B antes que C. El segundo, a B sobre C y a C sobre A. El tercero, a C sobre A y A sobre B.

Por tanto, si vot¨¢ramos por mayor¨ªa a los candidatos por pares, A ganar¨ªa a B (dos votos a uno), B ganar¨ªa a C (dos votos a uno) y C gana a A (dos votos a uno). Este ciclo de preferencias (A>B, B>C, C>A) es intransitivo, a pesar de que ninguno de los votantes ten¨ªa preferencias intransitivas. Como resultado de esta intransitividad, ser¨ªa posible dise?ar un sistema a dos vueltas que d¨¦ como ganador al candidato que queramos. Por ejemplo, si queremos que gane C, basta con establecer una primera ronda entre A y B y que el ganador (A) se enfrente a C. Del mismo modo, si queremos que gane A, establecer¨ªamos una primera ronda entre B y C, y el ganador (B) se enfrentar¨ªa a A.

El teorema de imposibilidad de Arrow profundiza en esta idea. El economista te¨®rico Kenneth Arrow demostr¨® que, bajo ciertas condiciones razonables, es imposible dise?ar un sistema de votaci¨®n que siempre genere resultados ¡°coherentes¡±. En otras palabras, no existe un sistema de votaci¨®n que satisfaga simult¨¢neamente todas las condiciones deseables en un sistema democr¨¢tico, como la no dictadura ¡ªno debe haber un votante cuya preferencia siempre prevalezca¡ª; la condici¨®n de Pareto ¡ªsi todos los individuos prefieren una opci¨®n sobre otra, el resultado colectivo tambi¨¦n debe reflejar esa preferencia un¨¢nime¡ª; y la independencia de alternativas irrelevantes ¡ªel resultado entre dos candidatos no debe depender de las preferencias de otros candidatos¡ª.

A pesar de estas limitaciones, otro resultado cl¨¢sico de Condorcet (el teorema del jurado) ofrece, a priori, una visi¨®n m¨¢s optimista sobre los procesos de decisi¨®n. Supongamos que nos enfrentamos a una decisi¨®n entre dos opciones y, a diferencia del caso anterior, existe una opci¨®n correcta. Por ejemplo, un jurado que debe tomar una decisi¨®n sobre la inocencia o culpabilidad de un acusado. Este teorema sugiere que, si cada votante tiene la misma probabilidad mayor al 50% de tomar la decisi¨®n correcta, entonces es m¨¢s probable que acierte un grupo de votantes independientes tomando una decisi¨®n por mayor¨ªa, en comparaci¨®n con un individuo por s¨ª solo. Adem¨¢s, a medida que el n¨²mero de votantes aumenta, la probabilidad de tomar la decisi¨®n correcta se acerca al 100%.

El economista Arrow demostr¨® que es imposible dise?ar un sistema de votaci¨®n ¡®coherente¡¯. En otras palabras, no existe un modelo que satisfaga simult¨¢neamente todas las condiciones deseables

Por ejemplo, supongamos que un jurado donde cada miembro tiene un 60% de probabilidad de tomar la decisi¨®n correcta. Sin embargo, como vemos en la figura, un jurado de 25 personas tendr¨ªa una probabilidad de casi el 85%.

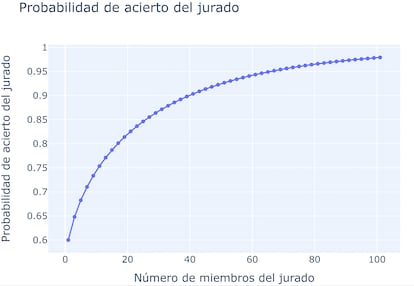
No obstante, no es realista pensar que todos los votantes tienen la misma probabilidad de acertar y esto es importante para aplicar el teorema. Dependiendo de las probabilidades de cada votante, la probabilidad del jurado de acertar tiende a uno o no, como plantea la tesis del teorema.

Recientemente, siguiendo un enfoque bayesiano, se ha estimado la probabilidad a priori de que la tesis predicha por el teorema se cumpla. Es decir, si elegimos una secuencia arbitraria de votantes con diferentes probabilidades de tomar la decisi¨®n correcta, ?se cumplir¨¢ que la probabilidad de acertar del jurado tiende al 100% a medida que aumentamos el n¨²mero de miembros? La respuesta es no. M¨¢s precisamente, si se toma una secuencia aleatoria de probabilidades siguiendo cualquier distribuci¨®n ¡°sim¨¦trica¡±, la tesis predicha por el teorema no se cumplir¨¢ en ¡°casi¡± todos los casos, esto es, se cumplir¨¢ con probabilidad cero.

Estos resultados matem¨¢ticos recuerdan la importancia de reflexionar sobre las estructuras y sistemas de votaci¨®n que utilizamos en nuestras sociedades. Al entender las fortalezas y debilidades de estos sistemas, podemos trabajar en mejorarlos y garantizar que nuestras democracias sean lo m¨¢s epist¨¦micamente eficientes posible.

?lvaro Romaniega es doctor en Matem¨¢ticas por el Instituto de Ciencias Matem¨¢ticas (ICMAT) y actualmente es investigador en finanzas estoc¨¢sticas.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.