De los hombres p¨¢jaro a los hermanos Wright: las matem¨¢ticas que nos ayudaron a surcar el aire

En estos momentos hay entre ocho mil y veinte mil aviones surcando el cielo simult¨¢neamente en el mundo. Cada uno de estos vuelos es posible gracias a las matem¨¢ticas, en aspectos que van desde la planificaci¨®n del consumo del combustible al dise?o y mejora de los aparatos. Los primeros veh¨ªculos que permitieron al ser humano alzarse sobre la superficie terrestre (globos aerost¨¢ticos, dirigibles, planeadores y aviones) se sustentaron en diversos conceptos geom¨¦tricos, algebraicos o anal¨ªticos.

En el siglo IX, los hombres p¨¢jaro se convirtieron en precursores de la aviaci¨®n. Sin un soporte te¨®rico y ¨²nicamente con la esperanza de poder volar, abr¨ªan las alas tejidas a sus trajes y se lanzaban de grandes alturas, fallando una y otra vez en el intento. Tras ellos, el primer vuelo en paraca¨ªdas, m¨¢s o menos exitoso, fue realizado por el qu¨ªmico, f¨ªsico y matem¨¢tico Abbas Ibn Firn¨¢s (810, Ronda; 887, C¨®rdoba) en ese mismo siglo, lo que sentar¨ªa las bases para los futuros dise?adores de aeronaves.

La trigonometr¨ªa y la geometr¨ªa cl¨¢sica desempe?aron un papel esencial en el estudio de la aviaci¨®n durante este primer periodo; permitieron a los pilotos y navegantes calcular distancias, ¨¢ngulos y altitudes con mayor precisi¨®n. En concreto, fueron clave los m¨¦todos trigonom¨¦tricos que el matem¨¢tico ¨¢rabe Al-Biruni hab¨ªa desarrollado entre los siglos X y XI para resolver problemas astron¨®micos y geod¨¦sicos, como la medici¨®n del radio de la Tierra.

Las primeras aeronaves que surcaron los cielos fueron las ¡°m¨¢s ligeras que el aire¡±, que se llenan con helio o hidr¨®geno, de manera que su peso total es menor que el peso del aire que desplazan. Ejemplos de estas aeronaves son el globo aerost¨¢tico, cuyo primer vuelo fue realizado por los hermanos Montgolfier; y el dirigible, dise?ado en Alemania por Ferdinard von Zeppelin. Para definir su dise?o y estabilidad se usaron los estudios sobre proporciones y vol¨²menes que Leonardo Fibonacci hab¨ªa hecho en los siglos XII y XIII. Tambi¨¦n se emplearon sus trabajos sobre proporciones arm¨®nicas, para establecer las dimensiones de diferentes componentes de las aeronaves (como las alas, fuselajes u otros elementos), lo que dio como resultado dise?os arm¨®nicos y est¨¦ticamente agradables.

En los siglos del XVIII al XIX, las investigaciones en geometr¨ªa permitieron desarrollar perfiles de alas m¨¢s eficientes. Un perfil aerodin¨¢mico es una forma geom¨¦trica, normalmente curva, presente en alas de aviones, aspas de helic¨®pteros, alerones y timones, dise?ada para optimizar el comportamiento de una superficie que interact¨²a con un flujo de aire, garantizando el menor arrastre posible causado por el viento.

Matem¨¢ticos como Daniel Bernoulli estudiaron la geometr¨ªa de las alas y tambi¨¦n otros aspectos estructurales, que buscaban lograr, por primera vez, el vuelo de una aeronave m¨¢s pesada que el aire. Aunque no lo consigui¨®, el trabajo de Bernoulli fue clave para comprender la interacci¨®n existente entre el aire y los objetos. De hecho, uno de los teoremas que propuso se sigue empleando hoy en d¨ªa en una de las explicaciones de por qu¨¦ vuelan los aviones. Este determina c¨®mo la velocidad del viento, al interactuar con las alas, causa una distribuci¨®n de presiones que elevan un avi¨®n.

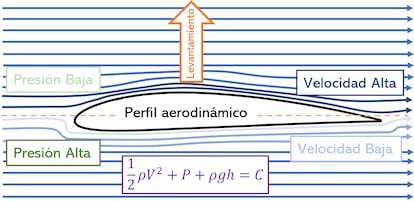
Otro enfoque frecuente para justificar el vuelo de las aeronaves recurre a la tercera ley de Isaac Newton: las part¨ªculas del viento son direccionadas hacia abajo, lo que causa la fuerza de levantamiento en el avi¨®n. Efectivamente, las leyes del movimiento y de la gravitaci¨®n universal formuladas por Newton en el siglo XVII (una descripci¨®n matem¨¢tica precisa de c¨®mo los cuerpos se mueven en el espacio) fueron la base para establecer los principios del vuelo de los aviones en tiempos cercanos a su invenci¨®n. Sin embargo, en la actualidad hay otras explicaciones m¨¢s aceptadas, basadas en el uso de la din¨¢mica de fluidos computacionales.

En 1799, el brit¨¢nico George Cayley desarroll¨® el perfil de ala sim¨¦trica, en el que la parte superior como la inferior son iguales, uno de los primeros perfiles aerodin¨¢micos reconocidos. Sin embargo, el verdadero avance en el dise?o de perfiles aerodin¨¢micos no se produjo hasta finales del siglo XIX, con nuevas investigaciones exhaustivas sobre la aerodin¨¢mica de las alas. Fue entonces cuando Otto Lilienthal realiz¨® numerosos vuelos en planeadores (aeronaves dise?adas para volar sin motor). A trav¨¦s de sus experimentos, recopil¨® datos y refin¨® perfiles aerodin¨¢micos que maximizaban la sustentaci¨®n y minimizaban la resistencia.

Unos a?os m¨¢s tarde, en 1903, los hermanos Wright fueron los primeros en lograr el vuelo motorizado controlado. Su trabajo, basado principalmente en experimentos con t¨²neles de viento, es la base en la comprensi¨®n de la forma de las palas en los motores turbof¨¢n, los m¨¢s utilizados en los aviones comerciales actualmente. Este tipo de motores contiene un ventilador de gran tama?o que comprime el aire entrante, el cual es mezclado con combustible, generando gases de alta velocidad que son expulsados para propulsar la aeronave. El dise?o ¨®ptimo de la geometr¨ªa de estos veh¨ªculos permite reducir la resistencia del aire, ahorrando combustible, reduciendo el ruido de los motores y evitando turbulencia durante los vuelos.

Desde comienzos del siglo pasado, la industria aeron¨¢utica ha evolucionado de manera abrupta gracias al uso de herramientas te¨®ricas y computacionales, diversos teoremas, ideas y teor¨ªas matem¨¢ticas que se emplean en el an¨¢lisis y la optimizaci¨®n de diversos aspectos de la aviaci¨®n. A esto dedicaremos un siguiente art¨ªculo de Caf¨¦ y Teoremas.

Yoshua D¨ªaz Interian es investigador predoctoral en el Instituto Polit¨¦cnico Nacional (M¨¦xico).

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n Garc¨ªa-Longoria. Es coordinadora de la Unidad de Cultura Matem¨¢tica del Instituto de Ciencias Matem¨¢ticas (ICMAT)

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.