D¡¯Alembert y el c¨¢lculo de probabilidades

Con su absurda ley procreativa, el rey machista de la semana pasada solo consigui¨® reducir dr¨¢sticamente el n¨²mero de sus s¨²bditos, pero la proporci¨®n de hombres y mujeres sigui¨® siendo la misma. Consideremos una muestra de 100 parejas que empiezan a procrear: entre sus primog¨¦nitos habr¨¢ aproximadamente 50 ni?os y 50 ni?as; los progenitores de las segundas ya no podr¨¢n tener m¨¢s descendencia; pero las otras 50 parejas, suponiendo que todas sigan procreando, tendr¨¢n aproximadamente 25 segundog¨¦nitos ni?os y 25 ni?as, y as¨ª sucesiva e ?indefinidamente? No: en principio, solo 12 o 13 parejas tendr¨¢n un tercer v¨¢stago, solo 6 o 7 tendr¨¢n un cuarto, solo 3 o 4 un quinto, solo 1 o 2 un sexto, y puede que ninguna un s¨¦ptimo. Cada ¡°remesa¡± de v¨¢stagos ser¨¢ la mitad de la anterior (y pronto se llegar¨¢ a la tasa de natalidad cero), pero en todas ellas habr¨¢ aproximadamente el mismo n¨²mero de ni?os que de ni?as.

A pesar de su sencillez, el problema suscit¨® un amplio debate, en el marco del cual Juan Jos¨¦ Rodr¨ªguez trajo a colaci¨®n las cr¨ªticas de d¡¯Alembert a la teor¨ªa de probabilidades convencional, que, seg¨²n ¨¦l, no prestaba la debida atenci¨®n a la experiencia al formular sus supuestos y sus definiciones. Lo cual, dicho sea de paso, hace m¨¢s dif¨ªcil de entender que el gran matem¨¢tico y enciclopedista franc¨¦s estimara, err¨®neamente, que la probabilidad de sacar al menos una cara al lanzar dos monedas al aire es 2/3. ?Cu¨¢l es la probabilidad real y qu¨¦ razonamiento enga?oso conduce al valor 2/3? Curiosamente, esta estimaci¨®n err¨®nea es un claro exponente de esa falta de atenci¨®n a las situaciones reales que el propio d¡¯Alembert criticaba.

Un ejemplo de lo complicado que puede ser a veces formular adecuadamente un problema de probabilidades lo encontramos en la paradoja de Bertrand (no me refiero a su famosa paradoja econ¨®mica relativa al equilibrio de Nash, sino a la probabil¨ªstica, de la que ya nos ocupamos hace unos a?os):

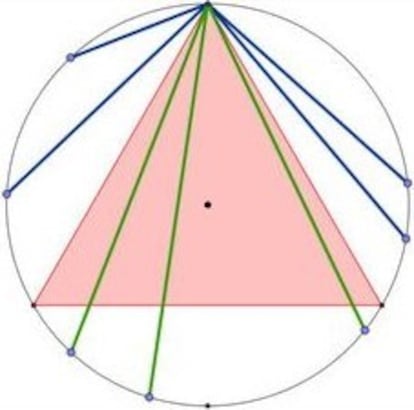
?Cu¨¢l es la probabilidad de que una cuerda trazada al azar en una circunferencia sea mayor que el lado del tri¨¢ngulo equil¨¢tero inscrito en ella? Seg¨²n como se aborde el problema, podemos llegar a distintas respuestas: 1/2, 1/3, 1/4¡­, e invito a mis sagaces lectoras/es a reconstruir los razonamientos que pueden llevarnos a estos u otros valores. Por ejemplo, ?cu¨¢l de las anteriores estimaciones sugiere la figura adjunta y por qu¨¦?

El hagad¨¢ de los caminantes sudorosos

La tradici¨®n oral nos ofrece numerosos e instructivos ejemplos de planteamientos err¨®neos, insuficientes, enga?osos o inveros¨ªmiles. En esta l¨ªnea, un conocido hagad¨¢ (cuento o f¨¢bula con moraleja de la tradici¨®n hebrea) habla de dos caminantes que -seg¨²n le refiere un rabino a su disc¨ªpulo- en un caluroso d¨ªa de verano van por un sendero polvoriento. Por fin encuentran una fuente donde calmar su sed. Uno de los caminantes tiene el rostro sucio de sudor y polvo, mientras que el otro lo tiene seco y limpio. ?Cu¨¢l de los dos se lava la cara?, pregunta el rabino.

La respuesta ingenua es que se lava la cara el que la tiene sucia. La respuesta ingeniosa es que se la lava el que la tiene limpia, pues cada uno ve el rostro de su compa?ero y no el propio, por lo que el que est¨¢ limpio cree que ¨¦l tambi¨¦n est¨¢ sucio y viceversa. Pero ?cu¨¢l ser¨ªa la respuesta realista, en la l¨ªnea cr¨ªtica de d¡¯Alembert (y del rabino del hagad¨¢)?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.