La paradoja de Bertrand

Con motivo de la entrega n¨²mero 200 de El juego de la ciencia, nos pregunt¨¢bamos la semana pasada si cambiando una cifra de este n¨²mero tan redondo y ¡°excesivo¡± podemos convertirlo en primo. Y la respuesta es no. Evidentemente, la cifra a cambiar tiene que ser la de las unidades, pues un n¨²mero terminado en 0 es divisible por 10, y esa ¨²ltima cifra no puede ser par, y tampoco puede ser 1, 5 ni 7, pues si la suma de las cifras de un n¨²mero es divisible por 3, lo es el propio n¨²mero. Los ¨²nicos candidatos son 203 y 209; pero 203 es divisible por 7, y 209 es divisible por 11; por lo tanto, no se puede convertir 200 en primo cambiando una de sus cifras. Y, por cierto, 200 es el menor n¨²mero con esta propiedad.

En cuanto a la secuencia 2, 10, 12, 16, 17, 18, 19, 200¡­, es la de los n¨²meros cuyo nombre empieza por la letra d.

El infinito y el azar

Todos tenemos -o creemos tener- una idea intuitiva de lo que es el azar, y tambi¨¦n sabemos que hay infinitos n¨²meros y que en una recta hay infinitos puntos. Pero cuando intentamos operar con estos escurridizos conceptos y llegar a conclusiones claras, nos encontramos a menudo con desconcertantes paradojas.

Una de las m¨¢s famosas es la paradoja de Bertrand, denominada as¨ª en honor del matem¨¢tico franc¨¦s Joseph Bertrand, que la expuso a finales del siglo XIX en su ya cl¨¢sico Calcul des probabilit¨¦s.

Para ilustrar su paradoja, Bertrand utiliz¨® un ejemplo que los lectores sacaron a relucir la semana pasada y que dio lugar a un animado e interesante debate (ver comentarios de ¡°El n¨²mero 200¡±). El ejemplo es el siguiente:

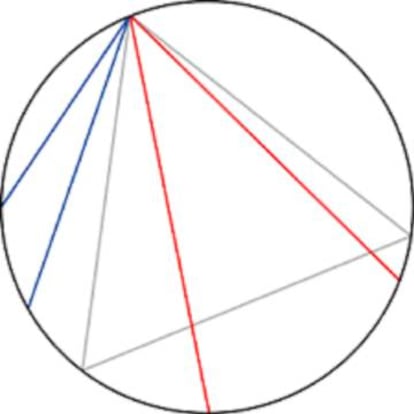
?Cu¨¢l es la probabilidad de que una cuerda trazada al azar en una circunferencia sea mayor que el lado del tri¨¢ngulo equil¨¢tero inscrito en ella?

Las cuerdas de todas las longitudes posibles pueden partir de un mismo punto cualquiera, puesto que todos los puntos de la circunferencia son equivalentes; consideraremos, pues, que uno de los extremos de la cuerda es uno de los v¨¦rtices del tri¨¢ngulo equil¨¢tero inscrito; si la cuerda cae dentro del tri¨¢ngulo, su longitud ser¨¢ mayor que el lado del mismo, y si cae fuera ser¨¢ menor, y como el ¨¢ngulo del tri¨¢ngulo equil¨¢tero es de 60? y todas las cuerdas posibles abarcan un ¨¢ngulo de 180? (pues el l¨ªmite est¨¢ en la tangente a la circunferencia en el v¨¦rtice que hemos tomado como origen), la probabilidad pedida ser¨¢ 60/180 = 1/3. Un razonamiento impecable; pero¡­

Consideremos ahora un radio perpendicular a un lado del tri¨¢ngulo inscrito. Todas las cuerdas perpendiculares a dicho radio que quedan entre el centro de la circunferencia y el lado del tri¨¢ngulo son mayores que ¨¦l, y todas las que quedan entre el lado y el otro extremo del radio son inferiores. Y como el lado del tri¨¢ngulo equil¨¢tero inscrito divide al radio en dos partes iguales, la probabilidad pedida ser¨¢ 1/2.

Y a¨²n hay otro criterio que nos da una probabilidad de 1/4, y todos los planteamientos parecen v¨¢lidos.

Invito a mis sagaces lectores/as a reflexionar sobre esta desconcertante paradoja y a proponer otros ejemplos de probabilidades parad¨®jicas o sorprendentes. Como este:

Si trazamos una circunferencia al azar en una hoja de papel cuadriculado, ?cu¨¢l es la probabilidad de que pase por alguno de los puntos de intersecci¨®n de la cuadr¨ªcula?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.