La excepci¨®n y la regla

El timbiriche o juego de ¡°puntos y cajas¡±, del que habl¨¢bamos la semana pasada, es m¨¢s dif¨ªcil de analizar de lo que sugiere su sencillo aspecto de pasatiempo infantil. Es tentador proponer, como hace Luca Tanganelli, la estrategia, para el segundo jugador, de trazar en cada turno el segmento sim¨¦trico -con respecto al centro del tablero- del trazado por el primero; pero esta estrategia, que funciona en otros juegos similares (como el de recubrir el tablero de ajedrez con fichas de domin¨®), en este caso falla, como muestra un sencillo contraejemplo enviado por Salva Fuster, que comenta: ¡°Creo que la argumentaci¨®n de la jugada sim¨¦trica tiene su inter¨¦s, pero me parece que la estrategia consiste en controlar la paridad de las cadenas de longitud mayor que 2. Creo que es una buena idea empezar por analizar el tablero de 4x4 puntos, es decir, de 9 casillas¡±.

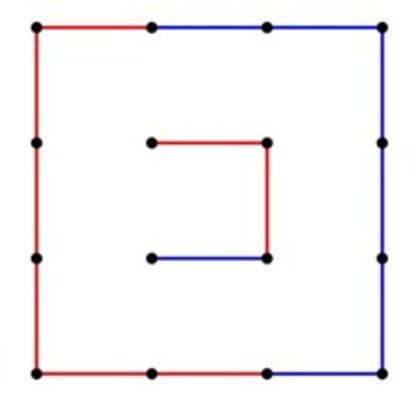
Si el segundo jugador (azul) juega sim¨¦tricamente, como se muestra en la figura, en su siguiente turno cierra el cuadradito central y pierde, pues acto seguido ha de trazar otro segmento que permitir¨¢ al rojo cerrar los ocho cuadraditos restantes. Descartada, pues, la estrategia sim¨¦trica, invito a mis sagaces lectoras/es a seguir jugando con los puntos y las cajas en busca de alguna generalizaci¨®n operativa.

Una refutaci¨®n demoledora

En matem¨¢ticas, la excepci¨®n no confirma la regla (por cierto, ?qu¨¦ sentido tiene la conocida expresi¨®n ¡°la excepci¨®n que confirma la regla¡±?), sino que la anula: basta un contraejemplo para invalidar una teor¨ªa, y el sencillo caso que acabamos de ver en relaci¨®n con el timbiriche nos lleva a pensar en ilustres y demoledoras refutaciones que han supuesto hitos en la evoluci¨®n de la ciencia y del pensamiento.

En este sentido, uno de los incidentes m¨¢s famosos fue el protagonizado por Bertrand Russell y Gottlob Frege a principios del siglo pasado. Tras veinte a?os de trabajo, en 1902 Frege hab¨ªa terminado el segundo volumen de su obra Las leyes fundamentales de la aritm¨¦tica, con la que pretend¨ªa dar a la matem¨¢tica un s¨®lido fundamento l¨®gico a partir de la teor¨ªa de conjuntos. El libro estaba ya en imprenta cuando Frege recibi¨® una carta de Russell en la que le comunicaba que hab¨ªa encontrado una paradoja en la teor¨ªa de conjuntos. A Frege solo le dio tiempo de insertar, al final de su libro, una nota con ribetes de esquela funeraria: ¡°Dif¨ªcilmente puede haber algo m¨¢s indeseable para un cient¨ªfico que ver derrumbarse los cimientos de su obra justo al terminarla. La carta del se?or Bertrand Russell me ha puesto en esa tesitura¡±.

Conceptualmente equivalente a la paradoja del barbero (en un pueblo hay un barbero que afeita a todos los que no se afeitan a s¨ª mismos, ?se afeita a s¨ª mismo el barbero?), la paradoja de Russell es la siguiente:

Llamemos normales a los conjuntos que no se contienen a s¨ª mismos y anormales a los que se contienen a s¨ª mismos. El conjunto de todos los conjuntos normales ?es normal o anormal? Si es normal, debe contenerse a s¨ª mismo (puesto que contiene todos los conjuntos normales), y por tanto es anormal, y si es anormal no debe contenerse a s¨ª mismo, luego es normal¡­

Invito a mis sagaces lectoras/es a encontrar una versi¨®n m¨¢s convincente y ajustada de la paradoja de Russell que la del barbero; por ejemplo, una versi¨®n bibliotecon¨®mica que involucre libros y cat¨¢logos (aunque cualquier otra versi¨®n ser¨¢ bien recibida).

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.