Las vacas de Narayana

Como cabe deducir de la correspondiente figura de la semana pasada, los n¨²meros de Narayana, N(n, k), se pueden interpretar como los distintos caminos de celos¨ªa que permiten ir de (0, 0) a (2n, 0) en 2n pasos recorriendo solo las diagonales de las celdillas y con k picos (se entiende por picos los v¨¦rtices superiores). Por lo tanto, N(4, 4) ser¨¢ el n¨²mero de recorridos entre (0, 0) y (8, 0) en 8 pasos y con 4 picos, y es f¨¢cil ver que solo hay un camino posible, el de la figura, por lo que N(4, 4) = 1.

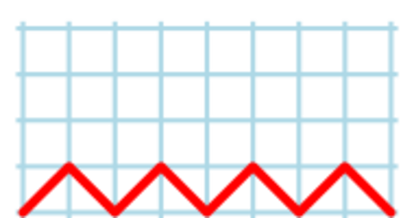
Ya sab¨ªamos, por la mencionada figura de la semana pasada, que N(4, 1) = 1, N(4, 2) = 6 y N(4, 3) = 6, y, como acabamos de ver, N(4, 4) = 1. Por lo tanto, los caminos posibles de la forma N(4, k), son, en total, 1 + 6 + 6 + 1 = 14 (recordemos que k no puede ser mayor que n, por lo tanto, solo puede tomar los valores 1, 2, 3 y 4). Seguro que los comentaristas habituales ven aqu¨ª una relaci¨®n directa con los n¨²meros de Catalan (?cu¨¢l es?).

Igualmente directa es la relaci¨®n de los n¨²meros de Narayana con las palabras de Dyck, de las que nos ocupamos recientemente (?puedes ver esa relaci¨®n entre n¨²meros y palabras?).

?rboles, palabras y n¨²meros

Hace unas semanas ve¨ªamos la relaci¨®n entre palabras de Dyck y ¨¢rboles binarios.

En la figura vemos tres ¨¢rboles enraizados ordenados (que parten de un nodo inicial llamado ra¨ªz y se ramifican de arriba abajo) de 4 aristas y 2 hojas (nodos terminales de los que no parte ning¨²n otro). ?Puedes dibujar alguno m¨¢s? ?C¨®mo se relacionan con los n¨²meros de Narayana?

Al igual que ocurre con los de Motzkin y los de Delannoy, no hay una f¨®rmula sencilla que d¨¦ N(n, k) en funci¨®n de n y k; hay que utilizar un doble sumatorio, o recurrir a los coeficientes binomiales.

El otro Narayana

Hasta ahora hemos hablado de T. V. Narayana (1930-1987), el matem¨¢tico canadiense de origen indio que descubri¨® los n¨²meros que llevan su nombre. Nombre que comparte con otro ilustre matem¨¢tico indio: Narayana Pandita (1340-1400), que en su tratado Ganita Kaumudi estudi¨® las que ¨¦l denomin¨® ¡°sucesiones aditivas¡±, en las que cada t¨¦rmino se obtiene mediante sumas a partir de los t¨¦rminos anteriores, y entre las que se encuentra la famosa sucesi¨®n de Fibonacci (y aunque Leonardo de Pisa es un par de siglos anterior, es muy probable que Narayana descubriera la misma sucesi¨®n independientemente).

En lugar de conejos, el matem¨¢tico indio utiliz¨® (mentalmente) vacas, m¨¢s acordes con su cultura, para ejemplificar una sucesi¨®n aditiva, planteando lo que desde entonces se conoce como el problema de las vacas de Narayana, que dice as¨ª:

Si las vacas tienen una cr¨ªa cada a?o, y cada ternera, despu¨¦s de los tres a?os que necesita para convertirse en una vaca madura, tiene una cr¨ªa a principio de cada a?o, ?cu¨¢ntas vacas habr¨¢ despu¨¦s de 20 a?os a partir de una primera ternera?

Invito a mis sagaces lectoras y lectores, no solo a calcular cu¨¢ntas vacas habr¨¢ al cabo de 20 a?os, sino tambi¨¦n a confeccionar una tabla con las vacas de cada generaci¨®n y a sacar las conclusiones pertinentes.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.