2023!

La relaci¨®n de los n¨²meros de Narayana con los de Catalan, planteada la semana pasada, es sencilla y directa:

Cn = N(n, 1) + N(n, 2) + N(n, 3) + ¡­ + N(n, n)

Como vimos, con sus correspondientes gr¨¢ficos, N(4, 1) + N(4, 2) + N(4, 3) + N(4, 4) = 1 + 6 + 6 + 1 = 14, que es precisamente C4. Y la relaci¨®n de los n¨²meros de Narayana con las palabras de Dyck es a¨²n m¨¢s directa (?cu¨¢l es?).

En la figura vemos los tres ¨¢rboles enraizados ordenados de cuatro aristas y dos hojas que completan, junto con los 3 de la semana pasada, los 6 posibles, n¨²mero que se corresponde con N(4, 2). En general, hay N(n, k) ¨¢rboles enraizados de n aristas y k hojas.

La secuencia de Narayana

En cuanto al problema de las vacas de Narayana, nuestras protagonistas de la semana pasada, si empezamos con una ternera reci¨¦n nacida a principios del primero a?o, durante tres a?os solo tendremos una vaca. El cuarto a?o la ternera se habr¨¢ convertido en vaca adulta y tendr¨¢ una cr¨ªa, y otra al quinto a?o, y otra al sexto. Al comienzo del s¨¦ptimo a?o la primera cr¨ªa ya estar¨¢ madura, por lo que nacer¨¢n dos terneras (la de la vaca originaria y la de su primera hija), y as¨ª sucesivamente. Obtenemos, as¨ª, la secuencia:

1, 1, 1, 2, 3, 4, 6, 9, 13, 19¡­

Es parecida, pero no igual, a la de Fibonacci:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55¡­

La segunda crece m¨¢s deprisa (ya se sabe, las conejas son mucho m¨¢s prol¨ªficas que las vacas), pues cada t¨¦rmino es la suma de los dos anteriores, mientras que en la primera cada t¨¦rmino es¡­ ?C¨®mo expresar¨ªas cada t¨¦rmino de la secuencia de Narayana en funci¨®n de los anteriores? ?Cu¨¢l ser¨ªa el vig¨¦simo t¨¦rmino de la secuencia? ?Cu¨¢ntas vacas tendr¨ªamos en total al cabo de 20 a?os?

En el problema, tal como lo plante¨® Narayama Pandita, se supone que todas las vacas viven a lo largo de todo el proceso, lo que significa que la primera vaca vivir¨¢ al menos 20 a?os, una estimaci¨®n optimista pero veros¨ªmil. M¨¢s pesimista, nuestro comentarista habitual Francisco Montesinos plantea una variante en la que las vacas solo viven 7 a?os (ver comentario 9 de la entrega anterior). ?Cu¨¢ntas vacas habr¨ªa, en ese caso, al cabo de 20 a?os?

En un interesante art¨ªculo (la referencia la dar¨¦ la semana que viene) encuentro esta tabla:

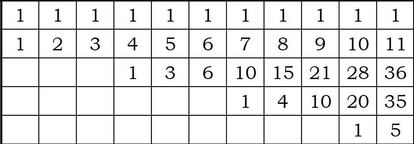
?Tiene algo que ver con el tema que nos ocupa? ?Qu¨¦ significa?

Un gran 2023!

Salvo error u omisi¨®n, esta entrega de El juego de la ciencia (la n¨²mero 395 en EL PA?S) se publicar¨¢ el 30 de diciembre, a las puertas del a?o 2023, por lo que no est¨¢ de m¨¢s echarle una ojeada al n¨²mero como tal. A primera vista, no parece muy interesante: no es primo, no es perfecto, no es poligonal, no es regular, no es factorial, no es un n¨²mero de Fibonacci ni de Catalan¡­ Podr¨ªa parecer esf¨¦nico, pues es el producto de tres primos: 2023 = 7 x 17 x 17, pero el 17 est¨¢ repetido, as¨ª que tampoco. ?Pueden mis sagaces lectoras y lectores descubrir alguna propiedad poco evidente de este n¨²mero que nos acompa?ar¨¢ durante 365 d¨ªas? En cualquier caso, os deseo un gran a?o en todos los aspectos.

Por cierto, al omitir el signo de admiraci¨®n inicial en ¡°Un gran 2023!¡±, no queda claro si os estoy felicitando el a?o nuevo a la italiana o aludiendo al tama?o del factorial de 2023. ?De qu¨¦ orden es 2023!? ?Con cu¨¢ntos ceros termina? ?Cu¨¢l es su primera cifra?

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.