Tolst¨®i y los segadores diligentes

La cuesti¨®n de la sombra del avi¨®n (o el dirigible), planteada la semana pasada a partir de un libro de Y¨¢kov Perelman, ha suscitado un extenso e intenso debate (ver comentarios de la entrega anterior). Empecemos por el final:

El ¡°metaproblema¡± de la dualidad avi¨®n-dirigible tiene que ver con el hecho de que el pr¨®logo corresponde a una edici¨®n muy posterior a la primera, de los a?os veinte del siglo pasado, cuando a¨²n era habitual ver dirigibles en el cielo. Es de suponer que luego Perelman plante¨® la cuesti¨®n con un avi¨®n, en el pr¨®logo de una edici¨®n de finales de los treinta, para actualizar un poco el libro. En cualquier caso, el dirigible es m¨¢s adecuado para plantear la cuesti¨®n, pues vuela (volaba: siguen existiendo, pero de forma vestigial) m¨¢s bajo que un avi¨®n y siempre se desplaza horizontalmente, y adem¨¢s es mucho m¨¢s grande, por lo que proyecta una sombra considerable. Al contrario que un avi¨®n, que en muchos casos no proyecta sombra alguna, y si la proyecta es mucho m¨¢s peque?a que el aparato (a no ser que vuele muy bajo). Veamos por qu¨¦:

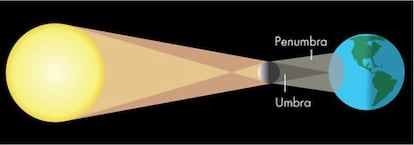
Es cierto que el Sol est¨¢ tan lejos (unos 150 millones de kil¨®metros) que podemos considerar que sus rayos son paralelos, por lo que hay que descartar el ¡°efecto divergencia¡± que agranda las sombras al iluminar algo con un foco puntual, como una linterna; pero el Sol es muy grande (1.400.000 km de di¨¢metro aproximadamente): su distancia a la Tierra equivale a solo unos 100 di¨¢metros solares, por lo que un observador terrestre forma con un di¨¢metro solar un tri¨¢ngulo is¨®sceles semejante a uno de 1 cm de base y 1 metro de altura; un tri¨¢ngulo muy estrecho y alargado, pero reconocible a simple vista y en absoluto irrelevante. Los objetos reciben la luz del Sol desde toda su superficie, y por eso forman un ¡°cono de sombra¡±. Por eso la Luna, durante un eclipse de Sol, proyecta sobre la superficie terrestre una sombra de unos pocos cientos de kil¨®metros de ancho como m¨¢ximo, cuando su di¨¢metro es de unos 3.500 km. Y por eso la sombra del dirigible ser¨¢ m¨¢s peque?a que la aeronave y la del avi¨®n, probablemente, ni siquiera llegar¨¢ a formarse.

Para comprobar a peque?a escala este fen¨®meno, como se?ala Ram¨®n Jaraba, basta con lanzar una pelota de tenis hacia arriba en un d¨ªa soleado: su sombra disminuye de tama?o, hasta desaparecer por completo, a medida que la bola asciende.

Problemas ilustres

Una de las muchas aportaciones de Y¨¢kov Perelman a la matem¨¢tica recreativa fue popularizar algunos problemas cl¨¢sicos y/o vinculados a grandes figuras del pensamiento, como Newton, Tolst¨®i o Einstein. En su libro ?lgebra recreativa, Perelman menciona, entre otros problemas ilustres, uno que al parecer era el preferido de Tolst¨®i, en el que se unen la afici¨®n del autor de Guerra y paz por las matem¨¢ticas con su inter¨¦s por la planificaci¨®n agr¨ªcola:

Un artel (asociaci¨®n voluntaria de trabajadores) de segadores ha de segar dos campos, uno de los cuales dobla al otro en superficie. Durante medio d¨ªa trabajan todos los segadores en el campo grande, y despu¨¦s de comer la mitad siguen en el campo grande y la otra mitad trabaja en el peque?o. Durante la tarde terminan de segar ambos campos casi por completo, a excepci¨®n de un reducido sector del campo peque?o, cuya siega ocupa a un solo segador durante todo el d¨ªa siguiente. ?Cu¨¢ntos segadores hab¨ªa en el artel?

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.