Billar din¨¢mico

Con respecto al problema del billar circular planteado la semana pasada, nuestro comentarista habitual Manuel Amor¨®s aporta la siguiente soluci¨®n:

¡°Consideremos dos bolas A y B situadas en el di¨¢metro de una mesa circular de radio R. Las bolas est¨¢n situadas a ambos lados del centro C (si est¨¢n al mismo lado solo existe la soluci¨®n trivial de tirar en la direcci¨®n del di¨¢metro). La bola A est¨¢ a la distancia a del centro y la bola B a la distancia b del centro.

Sea P el punto donde la bola A debe golpear en la mesa. Llamando ¦Á al ¨¢ngulo que forma CP con el di¨¢metro:

cos ¦Á = R(b-a)/(2ab)

El problema solo tiene soluci¨®n no trivial cuando dicho coseno est¨¢ entre -1 y 1¡å.

En el caso de las bolas situadas sobre un di¨¢metro y a ambos lados del centro de la mesa, no es dif¨ªcil hallar la soluci¨®n gr¨¢ficamente con regla y comp¨¢s (invito a mis sagaces lectoras/es a buscarla). Pero si las bolas de billar (o el foco de luz y el objeto a iluminar en el espejo circular) no est¨¢n sobre un mismo di¨¢metro, o sea, en el problema de Alhac¨¦n no simplificado, la construcci¨®n con regla y comp¨¢s no es posible, y al intentar resolverlo por la v¨ªa algebraica nos encontramos con una ecuaci¨®n de cuarto grado. Y no solo es dif¨ªcil resolver dicha ecuaci¨®n, sino incluso formularla, en contraste con la aparente sencillez gr¨¢fica del problema. Tan es as¨ª que, a finales del siglo XV, y tras buscar en vano una soluci¨®n matem¨¢tica del problema de Alhac¨¦n, Leonardo da Vinci propuso una soluci¨®n mec¨¢nica mediante un ingenioso pant¨®grafo dise?ado ad hoc. Una soluci¨®n algebraica no fue hallada hasta 1997, por el matem¨¢tico brit¨¢nico Peter M. Neumann.

El estadio de Bunim¨®vich y el billar de Sin¨¢i

Puesto que las ¨²ltimas semanas hemos hablado del billar rectangular convencional y del billar circular (menos convencional pero que tambi¨¦n existe f¨ªsicamente), es inexcusable hablar de la suma de ambos: el billar de Bunim¨®vich, ideado por el matem¨¢tico y f¨ªsico ruso-estadounidense Leonid Bunim¨®vich, conocido por sus importantes contribuciones al estudio de los sistemas din¨¢micos, que es un rect¨¢ngulo limitado por semic¨ªrculos en dos lados opuestos (por su forma, tambi¨¦n se conoce como estadio de Bunim¨®vich). No se trata de un billar f¨ªsico, sino ideal, y las ¡°bolas¡± son part¨ªculas puntuales con movimiento rectil¨ªneo y uniforme que al chocar con el contorno se reflejan especularmente sin p¨¦rdida de energ¨ªa (choque el¨¢stico), es decir, manteniendo siempre la misma velocidad. Es el m¨¢s conocido de los ¡°billares din¨¢micos¡±, que son idealizaciones del juego de billar con distintos contornos y eventuales obst¨¢culos internos. Su prop¨®sito es modelizar diversos tipos de movimientos de part¨ªculas y estudiar los sistemas hamiltonianos (pero ese es otro art¨ªculo).

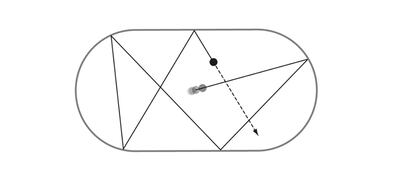
Otro famoso billar din¨¢mico es el ideado por Y¨¢kov Sin¨¢i, uno de los m¨¢s grandes matem¨¢ticos vivos (tambi¨¦n ruso-estadounidense, como Bunim¨®vich): es un cuadrado con un c¨ªrculo en su interior, en el que tambi¨¦n rebotan especularmente las part¨ªculas, y sirve entre otras cosas, para modelizar el comportamiento de un gas ideal.

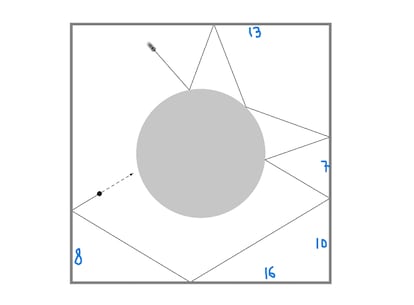
?Puedes determinar en qu¨¦ punto del per¨ªmetro cuadrado impactar¨¢ la part¨ªcula de la figura tras chocar por cuarta vez con el c¨ªrculo central del billar de Sin¨¢i? M¨¢s dif¨ªcil todav¨ªa: ?En qu¨¦ punto del c¨ªrculo chocar¨¢ por quinta vez? El lado del cuadrado mide 29 cm, el di¨¢metro del c¨ªrculo central mide 14 cm y los n¨²meros en azul indican las medidas de los segmentos correspondientes.

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.