Por qu¨¦ Espa?a tiene el doble de probabilidades de estar con Argentina o Brasil en el grupo del Mundial

El sorteo de la Copa del Mundo se celebra este viernes en Mosc¨² a las 16.00 (hora espa?ola), y ha llegado el momento de fijarse en las probabilidades de Espa?a. Este a?o la FIFA ha organizado los bombos de acuerdo con el nivel de los equipos (excepto en el caso de Rusia, la anfitriona) y no geogr¨¢ficamente.

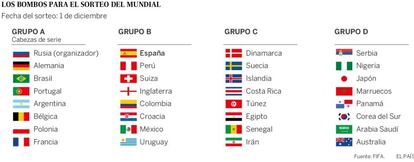
No obstante, va a seguir obligando a que dos selecciones del mismo continente, con la excepci¨®n de Europa, no puedan caer en el mismo grupo. Cada uno de los grupos deber¨¢ tener como m¨ªnimo uno y como m¨¢ximo dos equipos europeos. Esta restricci¨®n geogr¨¢fica tiene importantes repercusiones para las probabilidades del sorteo. Hay muchas maneras de hacer que se cumpla, y el lunes la FIFA dio a conocer el procedimiento oficial. El sistema pr¨¢cticamente reproduce las normas del sorteo de la Liga de Campeones, en el que los bombos 1 a 4 se vac¨ªan por ese orden y se cuenta con la ayuda de los ordenadores para evitar incompatibilidades geogr¨¢ficas.

Utilizando la norma oficial, he calculado las probabilidades de cada una de las 32 selecciones clasificadas en el sorteo bas¨¢ndome en 100.000 simulaciones. Estos son los resultados para Espa?a (las peque?as fluctuaciones en las probabilidades estimadas, llamadas ¡°error de estimaci¨®n¡±, se deben al n¨²mero finito de simulaciones):

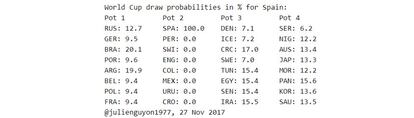
• Del bombo 1, Espa?a tiene un 20% de probabilidades de que le toquen Brasil y Argentina, y un 12,5% de que salga Rusia, pero solamente un 9,5% de que los elegidos sean Alemania, Portugal, B¨¦lgica, Polonia o Francia.
• Del bombo 3, es poco probable que a Espa?a le toquen Dinamarca, Islandia o Suecia (7% cada uno). El rival m¨¢s previsible es Costa Rica (17%), seguido de cerca por T¨²nez, Egipto, Senegal e Ir¨¢n (15,5% en cada caso).
• Del bombo 4, lo m¨¢s f¨¢cil es que La Roja evite a Serbia (6%). Su rival m¨¢s probable es Panam¨¢ (16%), seguido por los cuatro equipos asi¨¢ticos (Australia, Jap¨®n, Corea del Sur y Arabia Saud¨ª, con un 13,5% cada uno) y los dos africanos (Nigeria y Marruecos, con un 12%).

Como es l¨®gico, las probabilidades evolucionar¨¢n a lo largo del sorteo:

• Si Espa?a resulta emparejada con uno de los cabezas de serie europeos (60%), la probabilidad de que le toque un pa¨ªs escandinavo o Serbia se reducir¨¢ a cero. Al mismo tiempo, aumentar¨¢ la probabilidad de que en los bombos 3 y 4 salgan los otros equipos.
• Si le tocan Brasil o Argentina (40%), la probabilidad de que salgan Dinamarca, Islandia o Suecia en el bombo 3 se multiplicar¨¢ por m¨¢s de dos y se disparar¨¢ a alrededor de un 17,5% en cada caso. Tambi¨¦n aumentar¨¢ considerablemente la de que Serbia resulte elegida en el bombo 4 (15,5%). Ahora bien, como es l¨®gico, si a Espa?a le toca uno de los tres pa¨ªses escandinavos, no se permitir¨¢ que compita con Serbia.
• Si le toca Costa Rica en el bombo 3, no podr¨¢ enfrentarse a Panam¨¢. Y si le sale Ir¨¢n en ese mismo bombo, no podr¨¢ coincidir con los equipos asi¨¢ticos en el bombo 4. Lo mismo se puede decir de las selecciones africanas.

Las siguientes tablas muestran las probabilidades condicionales de Espa?a dependiendo de si le toca un cabeza de serie europeo o sudamericano. Son las tablas en las que habr¨¢ que fijarse durante el sorteo una vez que La Roja haya sido emparejada con uno de los primeros clasificados.

?C¨®mo es posible que las probabilidades de que le toquen rivales distintos, como Alemania y Brasil, en el bombo 1 sean tan diferentes? La respuesta se encuentra tanto en las restricciones geogr¨¢ficas como en la manera de obligar a que se cumplan. Como se explica en el v¨ªdeo del enlace,?cada vez que se extraiga un equipo de un bombo, ir¨¢ al primer grupo disponible (desde el A hasta el H) para el cual se pueda completar el sorteo sin que se produzca una incompatibilidad geogr¨¢fica.

Por ejemplo, imaginemos que Espa?a es el s¨¦ptimo equipo extra¨ªdo del bombo 2, que Uruguay es el que queda en ese mismo bombo, y que los dos favoritos disponibles son Alemania en el grupo G y Brasil en el grupo H. Incluso aunque, a priori, la selecci¨®n espa?ola podr¨ªa coincidir con ambos equipos, Espa?a se unir¨ªa al grupo de Brasil para evitar emparejar a Brasil y a Uruguay. El ejemplo ilustra por qu¨¦ es m¨¢s probable que a Espa?a (o a cualquier equipo europeo del bombo 2) le toque Brasil (o Argentina) que Alemania (o cualquiera de los cabezas de serie europeos).

El caso de Rusia es ligeramente distinto. Dado que fue incluida autom¨¢ticamente en el grupo 1, se emparejar¨¢ con la primera bola que se extraiga del bombo 2, lo cual significa que todos los equipos de este ¨²ltimo tienen una probabilidad entre ocho de que les toque Rusia.

En el caso de los bombos 1 y 2, otro procedimiento de sorteo podr¨ªa consistir en empezar por emparejar al azar los tres equipos sudamericanos del bombo 2 (Per¨², Colombia y Uruguay) con tres cabezas de serie europeos. A continuaci¨®n, las cinco selecciones restantes del bombo 2 ¡ªEspa?a entre ellas¡ª se emparejar¨ªan aleatoriamente con los cinco equipos que quedasen en el bombo 1 (Brasil, Argentina, y los tres cabezas de serie europeos). Esto tambi¨¦n dar¨ªa a Espa?a un 20% de probabilidades de enfrentarse a Brasil y Argentina, y solamente un 10% de jugar con cualquier favorito europeo. No obstante, ampliar este m¨¦todo a todos los bombos no es sencillo, y depende de la composici¨®n de estos. El procedimiento que imita al de la Liga de Campeones es m¨¢s coherente. Aun as¨ª, no es perfecto.

Como explicaba aqu¨ª, no todos los resultados completos admisibles del sorteo son igualmente probables. Algunos lo son un poco m¨¢s de lo que deber¨ªan, y otros menos. Hace tres a?os, propuse otro sencillo procedimiento de sorteo?que no solo elimina este sesgo, sino que adem¨¢s, al dividir los bombos en dos, resulta en grupos m¨¢s equilibrados. En este nuevo sistema, La Roja, al formar parte de la mitad m¨¢s fuerte del bombo 2, evitar¨ªa a equipos de la mitad m¨¢s fuerte del bombo 1, y en particular a Alemania y a Brasil.

Debido a las incoherencias de las clasificaciones de la FIFA, sigue siendo posible un ¡°grupo de la muerte¡± con Brasil, Espa?a, Suecia y Nigeria, sobre todo porque actualmente los rankings de la federaci¨®n infravaloran a Espa?a. No obstante, con el nuevo sistema de clasificaci¨®n, hay dos bombos (el 3 y el 4) sin ning¨²n equipo fuerte, lo cual supone que es mucho menos probable que se formen ¡°grupos de la muerte¡± que en el pasado.

Los ¡°grupos de la vida¡±, como ser¨ªa el caso de uno formado por Polonia o Rusia, Croacia, T¨²nez y Arabia Saud¨ª, seguir¨¢n siendo veros¨ªmiles. Aquellos en los que est¨¦n Rusia o Polonia probablemente ser¨¢n calificados de d¨¦biles. Polonia consigui¨® ser cabeza de serie en parte jugando inteligentemente las clasificaciones de la FIFA. El hecho de que solo se haya enfrentado en un amistoso entre noviembre de 2016 y octubre de 2017 ha hecho que suba en la clasificaci¨®n. Rusia es cabeza de serie dada su condici¨®n de anfitriona, pero actualmente no est¨¢ en muy buena forma.

Utilizar unos rankings mejores, as¨ª como tratar al anfitri¨®n como a cualquier otro equipo, contribuir¨ªa a equilibrar los grupos todav¨ªa m¨¢s. Los bombos ser¨ªan distintos si se empleasen los sistemas de puntuaci¨®n Elo en vez de los rankings de la FIFA y se clasificase a la anfitriona igual que a las dem¨¢s selecciones.

Espa?a, Inglaterra y Colombia sustituir¨ªan a Rusia, B¨¦lgica y Polonia como cabezas de serie, lo cual parece razonable. Espa?a ser¨ªa la m¨¢s beneficiada con el cambio, y se garantizar¨ªa que los grupos fuesen m¨¢s equilibrados, sobre todo si la FIFA utilizase el m¨¦todo propuesto por m¨ª. En ese caso, a Espa?a solamente le podr¨ªan tocar Croacia, M¨¦xico, Polonia o Dinamarca del bombo 2; Suecia, Ir¨¢n, Islandia o Senegal del 3, y Panam¨¢, Egipto, T¨²nez o Arabia Saud¨ª del 4.

Julien Guyon, matem¨¢tico franc¨¦s aficionado al f¨²tbol, es analista de datos y profesor adjunto en el departamento de Matem¨¢ticas de la Universidad de Columbia y en el Instituto Courant de Ciencias Matem¨¢ticas de la Universidad de Nueva York. Los m¨¦todos usados para las simulaciones est¨¢n descritos con detalle aqu¨ª. Las probabilidades del sorteo de las 32 selecciones est¨¢n disponibles en la cuenta de Twitter del autor, @julienguyon1977.