Por qu¨¦ el Barcelona tiene un 41,3% de probabilidades de emparejarse con el Chelsea en octavos

Los emparejamientos para la ronda de los octavos de final de la Liga de Campeones se sortear¨¢n el lunes, y este a?o algunas de las probabilidades del sorteo son bastante extremas. Por ejemplo, el Chelsea solo puede enfrentarse a tres equipos: Barcelona, Paris-Saint-Germain y Besiktas. El Chelsea tiene un 41,3% de posibilidades de que le toque el Barcelona, y un 29,4% de posibilidades de que le toque el PSG y el Besiktas.

Los otros posibles rivales del Barcelona (Basilea, Bayern de M¨²nich, Shakhtar Donetsk y Oporto) tienen casi las mismas posibilidades de tocarle (14-15%). Los rivales m¨¢s probables del Real Madrid son el AS Roma y el Liverpool, mientras que los del Sevilla son el AS Roma y el Tottenham (18,9% cada uno). Tanto el Real Madrid como el Sevilla tienen casi las mismas probabilidades de que les toquen los dos equipos de Manchester (18,3%). Los emparejamientos menos probables de todos son PSG-Oporto y Besiktas-Bayern (10,6%). En la siguiente tabla aparecen las probabilidades en el sorteo de los 16 equipos.

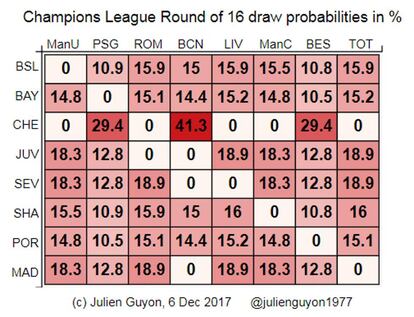
El hecho de que el Barcelona tenga tantas probabilidades de encontrarse con el Chelsea se debe a que el Chelsea solo puede enfrentarse a tres equipos, y a que el Barcelona solo puede hacerlo contra cinco. ?C¨®mo es que el Chelsea tiene tan pocos posibles rivales? Es la consecuencia de las limitaciones que impone la UEFA al sorteo: los ganadores de grupo deben emparejarse con los segundos de grupo; adem¨¢s, un equipo no puede jugar contra otro equipo de la misma federaci¨®n (pa¨ªs), ni tampoco contra un equipo al que se enfrent¨® durante la fase de grupos. Este a?o, excepcionalmente, Inglaterra cuenta con cinco representantes en la Liga de Campeones: los cuatro primeros de la Premier League del a?o pasado, m¨¢s el Manchester United, que se clasific¨® al ganar la Europa League. Cuatro de ellos ganaron en su grupo; solo el Chelsea acab¨® segundo de grupo, por detr¨¢s del AS Roma. Como consecuencia de ello, el Chelsea solo puede enfrentarse a los tres ganadores de grupo que no son ingleses (Barcelona, PSG y Besiktas), pero no al AS Roma.

Se podr¨ªa pensar que el Chelsea tiene un 33,3% de posibilidades de quedar emparejado con alguno de estos tres equipos, y es lo que pasar¨ªa si al Chelsea se le diese un trato especial al principio del sorteo: se elegir¨ªa una de las tres bolas (Barca, PSG, Besiktas) de un bombo para decidir el rival del Chelsea. Pero no es as¨ª como funciona el sorteo.

Tambi¨¦n se podr¨ªa pensar que, para calcular la probabilidad que tienen dos equipos A y B de enfrentarse, se deber¨ªa hacer primero una lista con todos los resultados admisibles del sorteo, es decir, los resultados que cumplan todas las limitaciones (hay 4.238), y luego se deber¨ªa calcular la proporci¨®n de estos 4.238 resultados en la que A y B se emparejan. Entre los 4.238 resultados posibles del sorteo, hay exactamente 1.854 resultados en los que el Chelsea se empareja con el Barcelona, lo que equivale a una proporci¨®n del 43,7%, mientras que solo hay 1.192 resultados en los que el Chelsea se empareja con el PSG o el Besiktas (28,1%). La raz¨®n por la que hay m¨¢s posibilidades de que al Chelsea le toque el Barcelona es que el Bar?a solo puede enfrentarse a cinco rivales (no puede enfrentarse a Juventus, Sevilla y Madrid), mientras que el PSG y el Besiktas pueden jugar contra siete.

Es tentador concluir que la probabilidad de un cruce Bar?a-Chelsea es del 43,7%. Ser¨ªa correcto si el sorteo consistiese en poner 4.238 bolas, una para cada sorteo admisible, en un bombo (muy grande) y en elegir una al azar para decidir todo el sorteo. Pero, naturalmente, esto no es factible. El sorteo no funciona as¨ª, por lo que el Bar?a y el Chelsea no tienen un 43,7% de posibilidades de enfrentarse en el sorteo.

Para calcular las probabilidades correctas del sorteo, se debe analizar el procedimiento del sorteo oficial que sigue la UEFA. En ¨¦l, se vac¨ªa en orden un bombo que contiene ocho bolas, una por cada segundo de grupo. Cada vez que sale un segundo, un ordenador enumera los rivales admisibles para cada equipo. Esto puede ser m¨¢s complicado de lo que se piensa. Supongamos, por ejemplo, que los tres primeros emparejamientos fuesen Barcelona-Oporto, Tottenham-Basilea y PSG-Sevilla. Luego, imaginemos que el Real Madrid es la cuarta bola que se extrae del bombo de los segundos. Aunque a priori le pueda corresponder el Besiktas, el ordenador considerar¨ªa que el Besiktas no es un rival posible para el Madrid. De hecho, emparejar al Madrid con los turcos llevar¨ªa a un callej¨®n sin salida: el Chelsea tendr¨ªa entonces que jugar contra un equipo ingl¨¦s o contra el AS Roma, que est¨¢ prohibido. Cuando aparece la lista, uno de los grupos admisibles se sortea al azar.

He calculado las probabilidades del sorteo simulando el sorteo cuatro millones de veces, seg¨²n el procedimiento del sorteo oficial. En realidad, tambi¨¦n es posible calcular las probabilidades exactas en un ordenador. Ambos m¨¦todos dan los mismos resultados, hasta el error de muestreo del m¨¦todo de simulaci¨®n. El procedimiento del sorteo influye en las probabilidades: un emparejamiento Bar?a-Chelsea es menos probable de lo que deber¨ªa ser (41,3% frente a 43,7%), mientras que los emparejamientos PSG-Chelsea y Besiktas-Chelsea son m¨¢s probables de lo que deber¨ªan ser (29,4% frente a 28,1%). Lo que quiero decir con ¡°deber¨ªa ser¡± es si los 4.238 resultados admisibles del sorteo fuesen igual de probables.

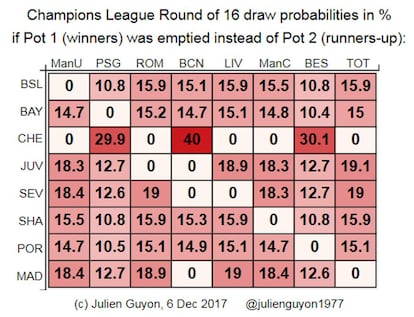
Para mostrar la influencia del procedimiento en las probabilidades, tambi¨¦n he calculado cu¨¢les ser¨ªan las probabilidades del sorteo si en vez de vaciar el bombo de los segundos, la UEFA vaciase el bombo de los ganadores de grupo (usando aqu¨ª 400.000 simulaciones). Sin duda, las probabilidades ser¨ªan ligeramente diferentes; por ejemplo, la probabilidad de un Bar?a-Chelsea disminuir¨ªa hasta el 40%.

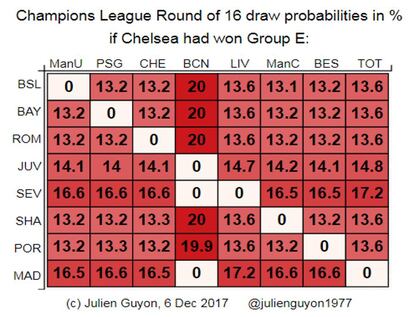
Por ¨²ltimo, tambi¨¦n he calculado cu¨¢les habr¨ªan sido las probabilidades del sorteo si el Chelsea hubiese ganado en su grupo (1 mill¨®n de simulaciones). Como pueden ver, las probabilidades habr¨ªan sido totalmente diferentes, no solo para el Chelsea, sino para todos los equipos. Es sorprendente que el resultado de un partido tenga tanta influencia sobre el resto de la competici¨®n.

Sin embargo, recuerden: el hecho de que el Barcelona tenga un 41,3% de posibilidades de enfrentarse al Chelsea tambi¨¦n significa que tiene m¨¢s posibilidades (58,7%) de no enfrentarse a ¨¦l.

Julien Guyon, matem¨¢tico franc¨¦s aficionado al f¨²tbol, es analista de datos y profesor adjunto en el departamento de Matem¨¢ticas de la Universidad de Columbia y en el Instituto Courant de Ciencias Matem¨¢ticas de la Universidad de Nueva York. Los m¨¦todos usados para las simulaciones est¨¢n descritos con detalle aqu¨ª. Hay m¨¢s tablas de probabilidades disponibles en la cuenta de Twitter del autor, @julienguyon1977.