Cantor, el Aleph y los distintos infinitos

Este blog, El Aleph, ha cumplido un a?o por estas fechas. Son ya 52 art¨ªculos los que se han publicado en ¨¦l (¨¦ste es el n¨²mero 53), y por ello creo que es el mejor momento para hablar sobre la relaci¨®n que tienen las matem¨¢ticas con el t¨ªtulo del mismo. Sirvan para ello los siguientes p¨¢rrafos.

El infinito es un concepto complicado de manejar y de entender (de hecho, dudo que haya alguien que sea capaz de comprenderlo en toda su extensi¨®n). Por ello, los acercamientos al concepto de infinito de siempre fueron poco profundos, tomando muchas licencias y, en ocasiones, llenos de errores e incorrecciones. Pero desde siempre fue el infinito, uno solo.

Corr¨ªa el a?o 1891 cuando Georg Cantor, matem¨¢tico alem¨¢n, hac¨ªa saltar la banca en lo que al tema del infinito se refiere: no hab¨ªa un ¨²nico infinito, sino muchos, todos ellos distintos, lo cual fue un aut¨¦ntico boom en la ¨¦poca (hasta el punto de no ser aceptado por muchos matem¨¢ticos hasta tiempo despu¨¦s).

Pero vayamos por partes. La cuesti¨®n clave de este asunto, demostrada por Cantor, es que los n¨²meros naturales y los n¨²meros reales tienen distintas cantidades infinitas de elementos. Como esto puede ser un poco complejo de entender, voy a intentar explicarlo de la manera m¨¢s clara posible. Pero antes vamos a dar nombre a algunas cosas.

Suele denominarse cardinal de un conjunto a la cantidad de elementos que tiene dicho conjunto. Es evidente que tanto el conjunto de los naturales como el conjunto de los reales tienen cardinal infinito, pero lo que advirti¨® (y demostr¨®) Cantor es que esos infinitos son esencialmente distintos.

La idea de Cantor para demostrar este hecho se suele llamar actualmente m¨¦todo diagonal de Cantor. Lo que hizo fue suponer que ambos cardinales eran iguales, lo que significa que a cada elemento de uno de los conjuntos podemos asignarle un elemento del otro conjunto, y viceversa, de manera que no sobra ning¨²n elemento en ninguno de los conjuntos (lo que se llama correspondencia biun¨ªvoca).

Habitualmente se hace esto entre el conjunto de los n¨²meros naturales, {1, 2, 3,¡­}, y los n¨²meros contenidos entre el 0 y el 1 (aprovechando que el intervalo (0,1) y el conjunto de los n¨²meros reales s¨ª que tienen el mismo cardinal). Lo que har¨ªamos ser¨ªa listar todos los elementos de este intervalo, cuesti¨®n que haremos expresando sus elementos como n¨²meros decimales, y asignar a cada n¨²mero natural uno de esos n¨²meros decimales. Una posible asignaci¨®n podr¨ªa comenzar as¨ª:

Si ambos conjuntos tuvieran el mismo cardinal, no habr¨ªa m¨¢s elementos en el intervalo (0,1) aparte de los que aparecen en esta asignaci¨®n (recordad que hemos listado todos los elementos de dicho intervalo). Bien, pues vamos a construir un n¨²mero que est¨¢ entre el 0 y el 1 pero no est¨¢ en la lista anterior.

Los decimales de este n¨²mero ser¨¢n de la siguiente forma: el primero, distinto al primer decimal del primer n¨²mero de la lista; el segundo, distinto del segundo decimal del segundo n¨²mero de la lista; el tercero, distinto del tercer decimal del tercer n¨²mero de la lista; y as¨ª sucesivamente. Por ejemplo, podemos tomar en cada caso el n¨²mero siguiente a cada decimal (si es un 3 tomamos un 4, si es un 8 tomamos un 9, y si es un 9 tomamos un 0). En nuestro caso, nos quedar¨ªa lo siguiente:

Part¨ªamos de una lista que supon¨ªamos completa y hemos construido un n¨²mero que est¨¢ entre 0 y 1, a=0¡¯49394340¡­, que no pertenece a dicha lista (difiere con todos los de nuestra lista en, al menos, un decimal). Esto es una contradicci¨®n, que parte de suponer que ambos conjuntos tienen el mismo cardinal (recordad el m¨¦todo de reducci¨®n al absurdo). Por tanto, los n¨²meros naturales y los n¨²meros reales tienen cardinales distintos, lo que nos lleva a que hay distintos tipos de infinito.

Los m¨¢s puristas advertir¨¢n en la demostraci¨®n anterior algunos peque?os ¡°problemas¡±, algunos detalles que ser¨ªa conveniente rellenar y algunas peque?as cuestiones con las que habr¨ªa que afinar algo m¨¢s de lo que lo he hecho yo. Esos detalles son f¨¢cilmente subsanables y hacerlo en este art¨ªculo resultar¨ªa demasiado engorroso teniendo en cuenta el prop¨®sito del mismo. Por ello, he preferido no incluirlos, pero os animo a que, si quer¨¦is, habl¨¦is sobre ellos en los comentarios.

?Qu¨¦ tiene que ver El Aleph en todo esto? Pues muy sencillo. El cardinal del conjunto de los n¨²meros naturales se denomin¨® aleph cero, y se representa mediante la letra hebrea aleph y un sub¨ªndice 0 para representar que el cardinal infinito m¨¢s peque?o.

Mediante razonamientos parecidos, se puede construir una sucesi¨®n de cardinales infinitos, cada vez mayores y estrictamente mayores que cada uno de los anteriores, que se nombran como aleph uno, aleph dos, etc.:

?Cu¨¢l es el cardinal del conjunto de los n¨²meros reales? Pues, por el tema de que los reales rellenan la recta de manera continua, se le llam¨® c (de continuo). Como pod¨¦is ver, este cardinal infinito no aparece en la lista anterior¡­o s¨ª, y me explico.

Por un lado, aleph uno es define como el menor cardinal infinito que es mayor que aleph cero, y por otro lado c (el cardinal de los n¨²meros reales) es tambi¨¦n mayor que aleph cero. Adem¨¢s, se sabe que el cardinal de los reales, c, es igual a 2 elevado a aleph cero. La pregunta que surge es la siguiente: ?son iguales? Bien, pues eso es lo que afirma la denominada hip¨®tesis del continuo:

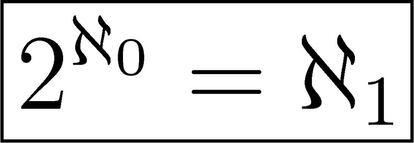
Cantor pensaba que era cierto que ambos cardinales son iguales, pero no fue capaz de demostrarlo. M¨¢s adelante, trabajos de Kurt G?del y Paul Cohen concluyeron que la hip¨®tesis del continuo es indecidible dentro de nuestra teor¨ªa de conjuntos, lo que significa que dentro de nuestra teor¨ªa de conjuntos (Zermelo-Fraenkel junto al axioma de elecci¨®n) no se puede ni demostrar ni refutar esta hip¨®tesis. Por tanto, podemos construir una teor¨ªa de conjuntos consistente donde la hip¨®tesis del continuo es cierta y otra, tambi¨¦n consistente, donde dicha hip¨®tesis es falsa. Casi nada.

Estos y otros trabajos de Cantor supusieron, como ya hemos comentado, una revoluci¨®n en las matem¨¢ticas de la ¨¦poca (de hecho, se considera a Georg Cantor como el creador de la moderna teor¨ªa de conjuntos). Fue complicado que los matem¨¢ticos de aquel momento aceptaran como ciertos los trabajos de Cantor, pero al final la matem¨¢tica tuvo que rendirse a las evidencias.

De Cantor y su trabajo habr¨ªa m¨¢s cosas que contar, pero eso lo dejaremos para pr¨®ximos art¨ªculos.