Brook Taylor, m¨²sico, pintor, jurista y gran matem¨¢tico

La llamada serie de Taylor no es tan medi¨¢tica como Juego de Tronos, pero resulta fundamental en el c¨¢lculo matem¨¢tico y, con ello, en el resto de ciencias e ingenier¨ªa. Su autor, el ingl¨¦s Brook Taylor, tampoco es tan conocido como otros cient¨ªficos, aunque cualquier estudiante de ingenier¨ªa u otras ciencias se ha enfrentado, en un inevitable curso de c¨¢lculo, a alguna de las criaturas matem¨¢ticas que llevan su nombre: la serie de Taylor, el polinomio de Taylor, la f¨®rmula de Taylor¡­ Sin embargo, su obra, o mejor dicho, sus intereses no se limitaron al quehacer matem¨¢tico. Estudi¨® leyes en Cambridge y recibi¨® una s¨®lida educaci¨®n musical y art¨ªstica, con varios tutores privados que se pod¨ªa permitir gracias a la holgada posici¨®n econ¨®mica de la familia.

M¨¢s informaci¨®n

Cient¨ªficos en guerra: Newton, Leibniz y el c¨¢lculo infinitesimal

El irresistible encanto de las matem¨¢ticas

Hace poco m¨¢s de 332 a?os, el 18 de agosto de 1685, nac¨ªa en Edmonton, una peque?a localidad de los alrededores de Londres, en el seno de una familia adinerada con extensas inquietudes art¨ªsticas e intelectuales. Su formaci¨®n polifac¨¦tica marc¨® una clara amplitud de miras a lo largo de su carrera. Trabaj¨® en diversos problemas fundamentales de las artes y las ciencias: estudi¨® el problema de la cuerda vibrante, fundamental para comprender el funcionamiento de instrumentos musicales como la guitarra o el piano, y cuya soluci¨®n requer¨ªa una considerable madurez matem¨¢tica; desarroll¨® el llamado m¨¦todo de las diferencias finitas, que permite resolver ciertas ecuaciones diferenciales mediante un sencillo procedimiento de ¨¢lgebra lineal; se interes¨® por temas de probabilidad, magnetismo, dise?o de term¨®metros, y un largo etc¨¦tera. En 1715, public¨® su tratado Linear Perspective que constituye uno de los primeros estudios formales sobre perspectiva y puntos de fuga.

Su vida ejemplifica la potente correlaci¨®n entre juventud y creaci¨®n matem¨¢tica: en 1712, con tan solo 27 a?os, ingres¨® en la prestigiosa Royal Society de Londres, y, tres a?os m¨¢s tarde, siendo secretario de esta sociedad, public¨® su obra Methodus incrementorum directa et inversa, en el que present¨® una de sus grandes aportaciones a las matem¨¢ticas: la serie de Taylor, que permite representar casi cualquier funci¨®n de una variable como una serie (una suma infinita). Esta t¨¦cnica permite aproximar muchas funciones por polinomios (sumas y restas de expresiones como ax, bx², cx³¡­), muy f¨¢ciles de calcular en t¨¦rminos de las derivadas sucesivas de la funci¨®n.

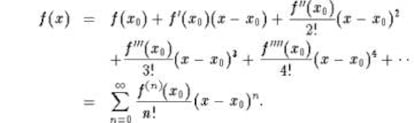
La serie de Taylor de la funci¨®n es el l¨ªmite de esa sucesi¨®n infinita de polinomios. Precisamente, llamamos funciones anal¨ªticas a aquellas para las que dicha serie es convergente cerca de cada punto. En la pr¨¢ctica, muchas funciones son anal¨ªticas, por lo que para aproximar la funci¨®n basta un n¨²mero finito de elementos de la serie (cuantos m¨¢s t¨¦rminos se consideren, se tendr¨¢n mejores aproximaciones a la propia funci¨®n). De hecho, el Teorema de Taylor proporciona una estimaci¨®n del error que se comete con la aproximaci¨®n en cada caso.

Seg¨²n los historiadores, existen precursores de las series de Taylor en los trabajos de la Escuela de Kerala de astronom¨ªa y matem¨¢ticas, del sur de India, durante los siglos XIV a XVI; y en las representaciones de funciones trigonom¨¦tricas descubiertas por el matem¨¢tico y astr¨®nomo escoc¨¦s James Gregory en el siglo XVII. Sin embargo, no hay duda de que el primero en formalizarlo con generalidad fue Taylor, aunque su trabajo permaneci¨® largo tiempo en el olvido, hasta que el matem¨¢tico franc¨¦s Joseph Louis de Lagrange lo rescatara en 1772, resaltando su importancia para el desarrollo del C¨¢lculo Diferencial. De hecho, Lagrange, e independientemente Augustin Louis Cauchy, profundizaron en la comprensi¨®n de las series de Taylor obteniendo expresiones expl¨ªcitas del error cometido en las aproximaciones, proporcionando la versi¨®n actual y m¨¢s completa del Teorema de Taylor.

Por su parte, sir Isaac Newton y Gottfried Leibniz, ambos autoproclamados fundadores del C¨¢lculo en una gran controversia durante el s. XVIII, tambi¨¦n desarrollaron sus propias versiones de lo que hoy se conoce como Teorema de Taylor. En el comit¨¦ constituido en 1712 para mediar en dicha disputa y atribuirle a cada uno lo suyo, se incluy¨® a un jovenc¨ªsimo Taylor, muestra de la especial relevancia y conocimiento que este ten¨ªa en el campo del c¨¢lculo.

Brook Taylor falleci¨® en Londres en 1731, a la edad de cuarenta y seis a?os, tras vivir una serie de tragedias familiares. No resulta dif¨ªcil imaginarse su epitafio: amante de la m¨²sica, pintor con talento, doctor en leyes y, en sus ratos libres, gran matem¨¢tico.

Pedro Tradacete es Profesor Visitante en el Departamento de Matem¨¢ticas de la Universidad Carlos III de Madrid.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.