La secuencia Look-and-say

Habl¨¢bamos la semana pasada sobre secuencias num¨¦ricas en ?Cu¨¢l es el siguiente t¨¦rmino? En ese art¨ªculo vimos ejemplos de secuencias num¨¦ricas interesantes y tambi¨¦n una forma de continuar cualquier secuencia num¨¦rica que nos propongan, dando adem¨¢s la regla que justifica la elecci¨®n que hagamos.

M¨¢s informaci¨®n

?Cu¨¢l es el siguiente t¨¦rmino?

L¨ªneas con nombre

El problema de los besos de las esferas

Tambi¨¦n propon¨ªamos dos secuencias para que los lectores las continuaran intentando adivinar la regla que se hab¨ªa usado para construirlas. La primera de ellas era la siguiente:

2, 10, 12, 16, 17, 18, 19,¡­

Como bien apuntaron Ozel Pociu e Ignacio Larrosa, el siguiente t¨¦rmino de la sucesi¨®n ser¨ªa el 200. De hecho, Ignacio dio algunos m¨¢s:

2, 10, 12, 16, 17, 18, 19, 200, 201, 202, 203,¡­

La regla de construcci¨®n de esta secuencia es muy sencilla: escribir de menor a mayor los n¨²meros que empiezan por la letra D al escribirlos en espa?ol. Como coment¨¢bamos en dicho art¨ªculo, es una secuencia muy conocida, pero no por ello deja de ser curiosa y apropiada para plante¨¢rsela a compa?eros y amigos para divertirse un rato pensando.

La segunda de las secuencias propuestas, que sirvi¨® para finalizar el art¨ªculo, era la siguiente:

1, 11, 21, 1211, 111221, 312211,¡­

Tambi¨¦n Ozel Pociu e Ignacio Larrosa continuaron bien la secuencia con el t¨¦rmino 13112221. La regla que se ped¨ªa encontrar para continuar esta secuencia es leer las cifras del n¨²mero (agrupando las que sean iguales) y escribir lo que hemos le¨ªdo tambi¨¦n en forma de n¨²mero.

Vamos a explicarlo un poco m¨¢s despacio. Comenzamos con 1, y ahora leemos las cifras del n¨²mero, agrupando las que sean iguales: ¡°un uno¡±. Ahora, escribimos en forma de n¨²mero lo que hemos le¨ªdo: 11.

Hacemos lo mismo, leemos este n¨²mero agrupando las cifras que sean iguales: ¡°dos unos¡±. Y ahora escribimos lo que hemos le¨ªdo: 21. Leemos de nuevo: ¡°un dos, un uno¡±. Por tanto, el siguiente t¨¦rmino es 1211. Y otra vez: ¡°un uno, un dos, dos unos¡±, lo que nos dice que el t¨¦rmino siguiente es el 111221. Y uno m¨¢s: ¡°tres unos, dos doses, un uno¡±, quedando ahora el 312211.

Haciendo lo mismo obtendr¨ªamos el siguiente t¨¦rmino, que es el que ped¨ªamos en el art¨ªculo anterior. Leemos: ¡°un tres, un uno, dos doses, dos unos¡±, y nos queda el que coment¨¢bamos unos p¨¢rrafos m¨¢s arriba: 13112221. Sabiendo ya la regla podemos continuar la secuencia. Aqu¨ª la ten¨¦is con unos cuantos t¨¦rminos m¨¢s:

Esta secuencia es conocida con el nombre de secuencia Look-and-say (A005150 en la OEIS), y es bastante interesante no solo por la curiosa manera en la que est¨¢ definida, sino por las propiedades que sabemos que cumple. Vamos a comentar algunas de ellas.

La primera es que la secuencia, tal cual la hemos descrito, cumple que sus t¨¦rminos van creciendo indefinidamente (pensad que podr¨ªa ser que al agrupar los n¨²meros consecutivos que sean iguales esto podr¨ªa no ser as¨ª). De hecho, esto ocurre comencemos con el n¨²mero que comencemos (hasta si es el cero), independientemente del n¨²mero de cifras que tenga¡­excepto si es el 22. ?Por qu¨¦? Muy sencillo, porque con el 22 obtenemos la siguiente secuencia:

22, 22, 22, 22, 22,¡­

Veamos otra curiosidad. Si os fij¨¢is en los t¨¦rminos que os he dado en la imagen anterior, solo aparecen unos, doses y treses. Bien, pues el caso es que est¨¢ demostrado que en ning¨²n t¨¦rmino de la sucesi¨®n aparecer¨¢ un n¨²mero mayor que 3 a no ser que el inicial contenga a dicho n¨²mero (o una cadena de m¨¢s de tres n¨²meros iguales consecutivos). Por ejemplo, si el inicial no tiene ning¨²n 7 ni siete n¨²meros iguales consecutivos, es imposible que aparezca un 7 en los t¨¦rminos posteriores.

Fij¨¦monos ahora no en los t¨¦rminos, sino en la cantidad de cifras que tiene cada uno de ellos. Veamos qu¨¦ ocurre si dividimos el n¨²mero de cifras de cada uno entre el n¨²mero de cifras del anterior:

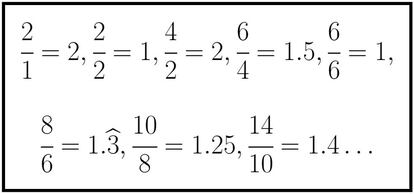
Bien, pues tambi¨¦n est¨¢ demostrado que dichas divisiones se van acercando al n¨²mero 1¡¯303577269034¡­ Dicho n¨²mero, que suele llamarse ¦Ë, es conocido como constante de Conway. De ¨¦l se sabe que es irracional y que, sorprendentemente, es algebraico (?qu¨¦ pens¨¢is que significa ese sorprendentemente?). Eso significa que es una de las soluciones de un cierto polinomio cuyos coeficientes son n¨²meros enteros.

Pero adem¨¢s sabemos exactamente cu¨¢l es ese polinomio. Concretamente, es este monstruo de grado 71:

A la vista del mismo, ?sabr¨ªas dar alguna raz¨®n que nos asegure que ¦Ë es irracional?

Todo lo que hemos comentado sobre la secuencia look-and-say lo sabemos gracias a los trabajos del gran matem¨¢tico brit¨¢nico John Horton Conway. Seg¨²n lo que sabemos, fue ¨¦l quien estudi¨® esta secuencia por primera vez y fue tambi¨¦n ¨¦l quien demostr¨® todas las propiedades que hemos comentado y alguna m¨¢s en The Weird and Wonderful Chemistry of Audioactive Decay.

Para finalizar, comentar que en dicho trabajo Conway tambi¨¦n demuestra que todos los t¨¦rminos de la secuencia que comienza con 1 pueden descomponerse en grupos de subt¨¦rminos, los cuales forman una lista de exactamente 92 elementos. En A derivation of Conway¡¯s Degree 71 ¡°Look-and-say¡± Polynomial ten¨¦is m¨¢s informaci¨®n al respecto.

No podr¨¦is negarme que esta secuencia look-and-say est¨¢ llena de curiosidad y de detalles que la hacen muy interesante. Y ahora os pregunto: ?conoc¨¦is alguna secuencia extra?a que tenga caracter¨ªsticas de inter¨¦s para hablar de ella aqu¨ª? Os agradeceremos que nos habl¨¦is de ellas en los comentarios.