Arqu¨ªmedes y la medida del c¨ªrculo

La conocida f¨®rmula de la longitud de la circunferencia, 2¦Ðr, en realidad es una tautolog¨ªa, puesto que ¦Ð es, por definici¨®n, la raz¨®n entre la circunferencia y su di¨¢metro (o lo que es lo mismo, 2r, dos veces el radio). Pero la no menos conocida f¨®rmula del ¨¢rea del c¨ªrculo, ¦Ðr², no es ni mucho menos evidente, y para dar con ella fue necesario todo el ingenio de uno de los m¨¢s grandes matem¨¢ticos de todos los tiempos.

En su libro Sobre la medida del c¨ªrculo, uno de los textos cient¨ªficos m¨¢s importantes de la antig¨¹edad, cuya influencia se prolong¨® a lo largo de siglos (a pesar de su brevedad y de no conservarse completo), Arqu¨ªmedes, anticip¨¢ndose en 2.000 a?os a los ¡°indivisibles¡± de Cavalieri y al c¨¢lculo infinitesimal de Leibniz y Newton, deduce la f¨®rmula del ¨¢rea del c¨ªrculo a la vez que halla un valor de ¦Ð incre¨ªblemente preciso. Pero empecemos por el principio¡­

La ¨²nica figura geom¨¦trica cuya f¨®rmula del ¨¢rea es evidente, es el rect¨¢ngulo, pues no hay m¨¢s que multiplicar la longitud de la base por la de la altura para hallar el n¨²mero de unidades cuadradas. Por ejemplo, si tenemos un rect¨¢ngulo de 5 cent¨ªmetros de base y 3 de altura, es evidente que contendr¨¢ 5 x 3 = 15 cuadraditos de 1 cent¨ªmetro de lado, o sea 15 cent¨ªmetros cuadrados. Generalizando, la superficie (S) de un rect¨¢ngulo de base b y altura a ser¨¢ S = b.a.

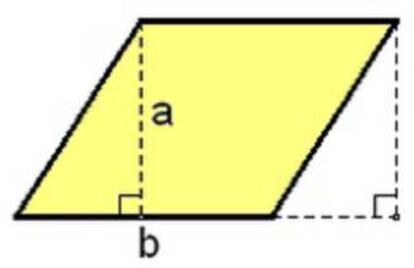
Es f¨¢cil ver que cualquier paralelogramo se puede convertir en un rect¨¢ngulo ¡°cortando¡± un tri¨¢ngulo rect¨¢ngulo de un extremo y ¡°peg¨¢ndolo¡± en el otro, por lo que tambi¨¦n en este caso el ¨¢rea se obtendr¨¢ multiplicando la base por la altura: S = b.a.

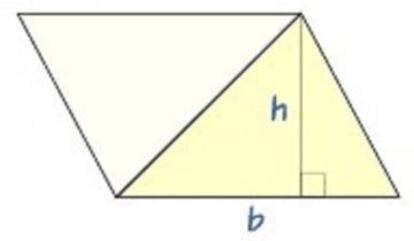
Y puesto que cualquier tri¨¢ngulo puede considerarse la mitad de un paralelogramo de igual base y altura (que podemos obtener trazando por dos de los v¨¦rtices sendas paralelas a los lados opuestos, como muestra la figura), el ¨¢rea de un tri¨¢ngulo ser¨¢ b.h/2 (la altura suele designarse indistintamente con las letras a o h).

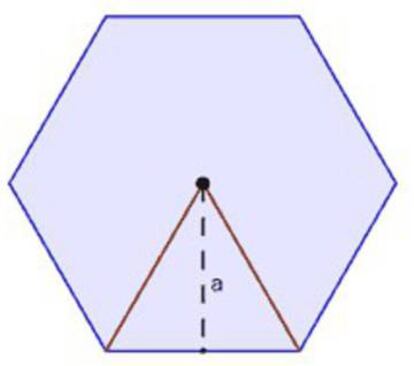
En el caso de un pol¨ªgono regular, como el hex¨¢gono de la figura, que tiene todos sus lados y todos sus ¨¢ngulos iguales, podemos dividirlo, trazando sus radios, en tantos tri¨¢ngulos is¨®sceles iguales (que en el caso del hex¨¢gono ser¨¢n equil¨¢teros) como lados tiene. Por lo tanto, su ¨¢rea ser¨¢ n.l.a/2, siento n el n¨²mero de lados, l el lado del pol¨ªgono y a la altura de cada tri¨¢ngulo, que es la apotema del pol¨ªgono; pero n.l es el per¨ªmetro (p) del pol¨ªgono, luego su ¨¢rea ser¨¢ p.a/2.

Para hallar el valor de ¦Ð, Arqu¨ªmedes imagin¨® un c¨ªrculo encerrado entre un pol¨ªgono inscrito y uno circunscrito de un n¨²mero de lados cada vez mayor. Obviamente, la longitud de la circunferencia ten¨ªa que ser siempre mayor que el per¨ªmetro del pol¨ªgono inscrito y menor que el per¨ªmetro del pol¨ªgono circunscrito, y a partir de sendos pol¨ªgonos de 96 lados respectivamente inscrito y circunscrito, hall¨® un valor de ¦Ð comprendido entre las fracciones 223/71 y 22/7; la media de estos dos valores es aproximadamente 3,1418, lo que significa que en el valor hallado por Arqu¨ªmedes el error es de apenas dos diezmil¨¦simas.

Y aunque el razonamiento mediante el cual el gran matem¨¢tico griego llega a la f¨®rmula del ¨¢rea del c¨ªrculo es algo m¨¢s largo y elaborado, en ¨²ltima instancia equivale a considerar que el c¨ªrculo es un pol¨ªgono regular de infinitos lados infinitamente peque?os, por lo que su apotema es el radio del c¨ªrculo y su per¨ªmetro la longitud de la circunferencia, con lo que la f¨®rmula p.a/2 se convierte en 2¦Ðr.r/2 = ¦Ðr².

Es curiosa la forma en que Arqu¨ªmedes presenta el ¨¢rea del c¨ªrculo, diciendo que es igual a la de un tri¨¢ngulo rect¨¢ngulo cuyos catetos son, respectivamente, el radio del c¨ªrculo y la longitud de su circunferencia. Un gui?o al viejo problema de la cuadratura del c¨ªrculo, aunque seguramente Arqu¨ªmedes ya sab¨ªa que era irresoluble. Pero esa es otra cuesti¨®n¡­

F¨®rmulas Magistrales es un secci¨®n de Carlo Frabetti dedicada a explicar las principales f¨®rmulas de las matem¨¢ticas y la f¨ªsica, su origen, evoluci¨®n y significado preciso.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra Newsletter