Siempre hay alg¨²n punto sin viento sobre la Tierra

En las previsiones meteorol¨®gicas de televisi¨®n suele mostrarse el mapa del viento. En ella aparecen sobre la Pen¨ªnsula una serie de flechas (vectores) superpuestas que indican la direcci¨®n y la intensidad del viento en el punto correspondiente. Si extendi¨¦ramos el mapa a toda la esfera podemos garantizar que en cualquier momento del d¨ªa habr¨¢ al menos un lugar en el que no sopla nada de viento. As¨ª lo determina el llamado teorema de la bola peluda, demostrado a principios del s. XX.

Matem¨¢ticamente, el mapa del viento corresponde a un campo de vectores sobre una superficie. ?ste asigna a cada punto de la superficie un vector tangente a la misma, de tal modo que puntos cercanos tienen asociados vectores parecidos, tanto en direcci¨®n como en longitud. A algunos puntos de la superficie se puede asignar el vector de longitud cero: ser¨¢n los puntos cr¨ªticos del campo de vectores. En el ejemplo meteorol¨®gico, esos ser¨ªan los lugares donde no sopla el viento.

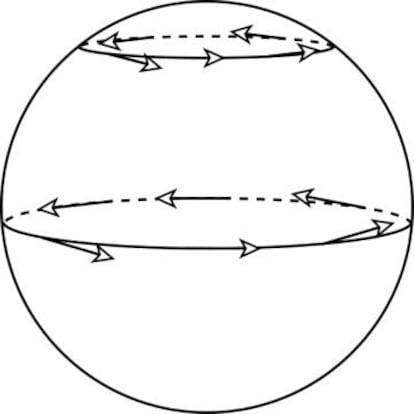
Sobre el mapa de Espa?a es f¨¢cil dibujar un campo de vectores sin puntos cr¨ªticos: por ejemplo, podr¨ªamos asignar a cada punto una flecha que apunte al Este. Pero al extender este campo a la totalidad de la superficie de la Tierra (ver ilustraci¨®n 1), el polo norte y el polo sur ser¨ªan puntos cr¨ªticos. En efecto, en ambos polos habr¨ªa que buscar un vector con una direcci¨®n parecida a la de los vectores cercanos, pero en los paralelos m¨¢s pr¨®ximos hay vectores que apuntan en infinitas direcciones distintas, as¨ª que para cumplir las condiciones establecidas solo es posible tomar un vector de longitud cero.

De hecho, para cualquier campo definido sobre la esfera, aparecer¨¢ al menos un punto de este tipo. Esta afirmaci¨®n se conoce de forma popular como el Teorema de la Bola Peluda, y es habitualmente interpretado diciendo que, no importa c¨®mo se peine una cabeza, siempre aparece un remolino. ?Algo que, cualquiera que haya peinado alguna vez a un/a ni?o/a, sabe a la perfecci¨®n! Es consecuencia de uno de los resultados m¨¢s importantes de la topolog¨ªa diferencial, el teorema de Poincar¨¦-Hopf, demostrado por el franc¨¦s Henri Poincar¨¦ en el caso de superficies y generalizado por Heinz Hopf a espacios de mayor dimensi¨®n.

El teorema de Poincar¨¦-Hopf determina, de forma general, sobre qu¨¦ tipo de espacios es posible construir un campo de vectores sin puntos cr¨ªticos. En concreto se aplica a superficies cerradas, es decir, aquellas que se pueden deformar (sin cortar ni pegar) en una esfera con un n¨²mero finito (que tambi¨¦n puede ser cero) de asas, o agujeros. Relaciona conceptos matem¨¢ticos a priori diferentes: el campo de vectores y la forma intr¨ªnseca (la topolog¨ªa) de una superficie.

Seg¨²n el teorema, dado un campo de vectores con un n¨²mero finito de puntos cr¨ªticos sobre una superficie cerrada con g asas los ¨ªndices de todos los puntos cr¨ªticos suman exactamente 2 ¨C 2g. El ¨ªndice de un punto cr¨ªtico de un campo de vectores es un n¨²mero entero distinto de cero que describe el comportamiento del campo de vectores en puntos muy pr¨®ximos al punto cr¨ªtico en cuesti¨®n.

En el caso de la esfera (que tiene cero agujeros), el teorema asegura que, para cualquier campo de vectores, la suma de los ¨ªndices de todos los puntos cr¨ªticos es 2. Por tanto, al menos tiene que haber uno ya que, evidentemente, si no hubiera ninguno, la suma ser¨ªa cero. En general, excepto para las superficies cerradas con una sola asa, la suma siempre ser¨¢ distinta de cero, y por tanto cualquier campo vectorial definido sobre ellas tendr¨¢ alg¨²n punto cr¨ªtico. El caso de un agujero se corresponde con el donut (llamado toro, en matem¨¢ticas). Aplicando el teorema sabemos que la suma de los ¨ªndices de los puntos cr¨ªticos de cualquier campo vectorial es siempre cero. Esto no garantiza que haya alguno sin puntos cr¨ªticos, pero tampoco lo impide, como sucede en el resto de casos.

De hecho, s¨ª es posible definir un campo sin puntos cr¨ªticos sobre el toro. Para ello dibujamos, primero, un campo de vectores sin puntos cr¨ªticos sobre una circunferencia (ver los c¨ªrculos marcados en la ilustraci¨®n 1). Como el toro es el resultado de rotar una circunferencia en el espacio tridimensional, basta rotar el campo que hab¨ªamos dibujado la circunferencia para obtener uno del toro. Por tanto, y por si alguien se hab¨ªa planteado la pregunta: s¨ª, es posible peinar un donut sin que quede ning¨²n remolino.?

Javier Aramayona es investigador Ram¨®n y Cajal en la Universidad Aut¨®noma de Madrid y miembro del ICMAT.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).