Una conjetura para controlar todos los espacios

La teor¨ªa de control es una de esas cosas de la vida que es f¨¢cil en la teor¨ªa y dif¨ªcil en la pr¨¢ctica. Por ejemplo, controlar un patinete, incluso en una pista lisa, es complicado para alguien que no tenga pr¨¢ctica. Sin embargo, resulta f¨¢cil explicar el fundamento te¨®rico: el sistema que controla la direcci¨®n del patinete (inclinar el cuerpo a la derecha y a la izquierda muy sutilmente y darse impulso con un pie) permite movimientos limitados: no puedes desplazar el patinete en direcci¨®n perpendicular a la de su movimiento. Lo bueno es que, pese a esta restricci¨®n, podemos ir de cualquier punto de la pista a otro. Es lo que en matem¨¢ticas se llama un sistema controlable.

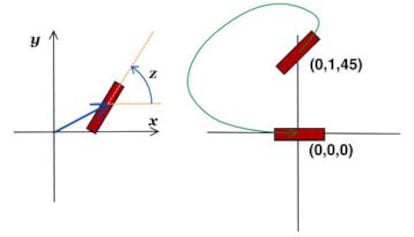
Para describir matem¨¢ticamente un sistema se recurre a la geometr¨ªa. El patinete vendr¨¢ dado por tres coordenadas: la posici¨®n (x,y) en el plano y el ¨¢ngulo de su eje, que llamamos z. Desplazar el patinete del punto (0, 1, 45) al (0,0,0), equivale a partir de una posici¨®n inicial (0,1) en la que el patinete forma 45 grados y ponerlo horizontal y bajar un metro en vertical. Es posible seguir en una trayectoria que conecte estos dos puntos y que no te lleve al hospital, que llamaremos curva admisible. Lo ideal ser¨ªa que pudi¨¦semos desplazarnos en nuestro espacio a lo largo de la l¨ªnea recta que une los dos puntos en el tres espacio, pero esto no suele ser as¨ª. En el ejemplo anterior, si sigui¨¦ramos la l¨ªnea recta har¨ªamos avanzar el patinete en una direcci¨®n que forma 45 grados con las ruedas y eso no es buena idea.

En general, para cualquier punto (x,y,z) de la pista existen solo algunas trayectorias (x(t), y(t), z(t)) ¨Cya que dependen del tiempo¨C admisibles. ?Podr¨ªamos saber cu¨¢les son? Pensando un poco, vemos que la clave es que sigan la direcci¨®n de los ruedas, lo que matem¨¢ticamente se traduce de la siguiente forma: valen las trayectorias cuya tangente a la curva posici¨®n en el punto (x(t), y(t)) tiene que formar ¨¢ngulo z(t).

Si consideramos un espacio formado por todas las curvas que pasan por un punto (x, y, z), estas curvas admisibles ser¨¢n un subconjunto, definido como las que son tangentes a un plano espec¨ªfico. Como el plano tangente permitido depende del punto, eso permite encontrar siempre curvas admisibles que conecten pares de puntos arbitrarios: podemos afirmar que el sistema de control geom¨¦trico es controlable.

El ejemplo del patinete muestra que en el espacio de tres dimensiones siempre es posible construir un sistema controlable. Pero ?podemos afirmar lo mismo en espacios de forma y dimensi¨®n generales? Gracias a una rama de la geometr¨ªa llamada topolog¨ªa simpl¨¦ctica sabemos que los sistemas m¨¢s controlables ¨Cdenominados estructuras de contacto¨C solo se pueden definir en espacios de dimensi¨®n impar.

Si consideramos un espacio formado por todas las curvas que pasan por un punto (x, y, z), estas curvas admisibles ser¨¢n un subconjunto, definido como las que son tangentes a un plano espec¨ªfico

A mediados del siglo XX el chino-americano Shiing-Shen Chern, considerado uno de los matem¨¢ticos m¨¢s importantes del siglo XX y padre de la geometr¨ªa diferencial moderna, conjetur¨® que en casi todos los espacios de dimensi¨®n impar existen estructuras de contacto; es decir, podemos crear un patinete que nos lleve a todas partes.

La demostraci¨®n se demor¨® m¨¢s 50 a?os y en sus sucesivos avances intervinieron muchos matem¨¢ticos ¨Centre ellos William Thurston, ganador de la Medalla Fields en 1982 o Mija¨ªl Gromov, premio Abel en 2009¨C. En 2015, el grupo de geometr¨ªa de contacto del ICMAT dio el paso definitivo para llegar a la respuesta general: prob¨® el caso de espacios de dimensi¨®n 5 ¨Cpasar de 3 a 5 resultaba ser lo m¨¢s complicado¨C. Adem¨¢s, en 2019 han explicado la prueba general en t¨¦rminos muy simples.

Con esta demostraci¨®n ya se puede garantizar que existen patinetes manejables en cualquier espacio. Eso s¨ª, de su manejo ¡°inteligente¡± ya se ocupa su conductor y, en todo caso, con la ayuda de otra rama de las matem¨¢ticas: la teor¨ªa de optimizaci¨®n.

Francisco Presas es cient¨ªfico titular del CSIC en el ICMAT

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter